Thermodynamics of metabolic energy conversion under muscle load

This paper is part of the analysis of the metabolic behaviour of living system. It constitutes the theoretical side of our approach, which relies on the formalism of Finite Time Thermodynamics, FTT, to give a solid basis to the phenomenological behaviours observed in the case of muscle. This work is directly related to the notion of the range of adaptation of a living organism to its environment, which we are developing in a series of other articles currently being written.

Author

Christophe Goupil, Henni Ouerdane, Eric Herbert, Clémence Goupil and Yves D’Angelo

Download

The paper were can be found using DOI or here

Abstract

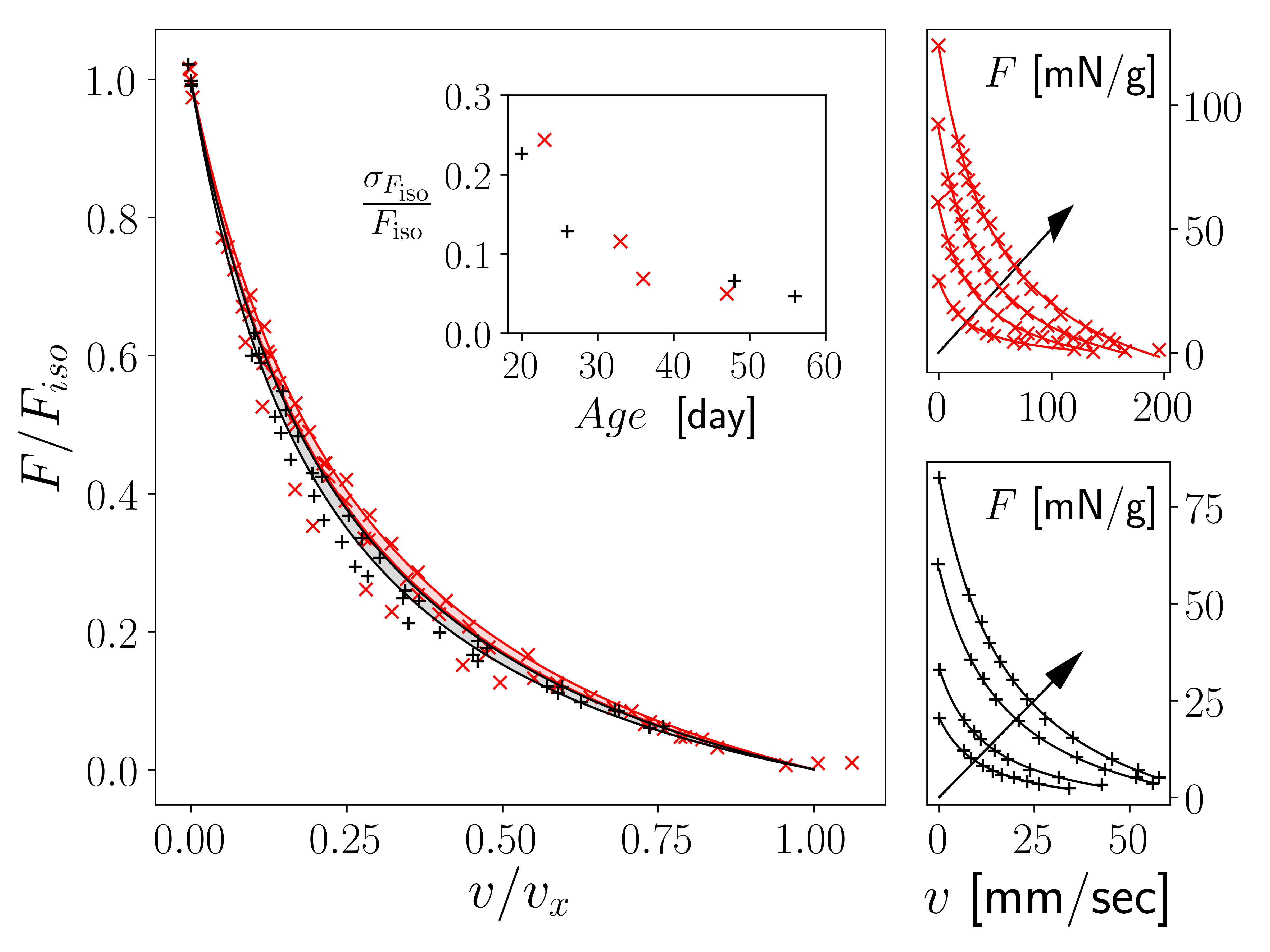
The metabolic processes complexity is at the heart of energy conversion in living organisms and forms a huge obstacle to develop tractable thermodynamic metabolism models. By raising our analysis to a higher level of abstraction, we develop a compact—i.e. relying on a reduced set of parameters—thermodynamic model of metabolism, in order to analyse the chemical-to-mechanical energy conversion under muscle load, and give a thermodynamic ground to Hill’s seminal muscular operational response model. Living organisms are viewed as dynamical systems experiencing a feedback loop in the sense that they can be considered as thermodynamic systems subjected to mixed boundary conditions, coupling both potentials and fluxes. Starting from a rigorous derivation of generalized thermoelastic and transport coefficients, leading to the definition of a metabolic figure of merit, we establish the expression of the chemical-mechanical coupling, and specify the nature of the dissipative mechanism and the so-called figure of merit. The particular nature of the boundary conditions of such a system reveals the presence of a feedback resistance, representing an active parameter, which is crucial for the proper interpretation of the muscle response under effort in the framework of Hill’s model. We also develop an exergy analysis of the so-called maximum power principle, here understood as a particular configuration of an out-of-equilibrium system, with no supplemental extremal principle involved.

Légende à ajouter