29 Oct 2025
We are always looking for motivated students. Don’t hesitate to contact us
Growing and Branching Network
Apex–Hypha Interaction.
The growth of filamentous fungal hyphae is polarized. In the vicinity of a pre-existing hypha, the growing tip exhibits either avoidance or attraction behavior.
Based on reconstructed data of thallus growth in a filamentous fungus, this project aims to characterize the nature and dynamics of these interactions.
| hyphal interactions |
 |
Out-of-Equilibrium Thermodynamics
-
Muscle is an energy-converting machine that can be described using Onsager’s classical Force–Flux formalism.
We propose to extend this framework in two main directions:
The current model applies only to stationary states. Building upon the time-dependent coupling matrices introduced by Zwanzig, we aim to describe transient phases of muscular acceleration.
The model is currently validated from the fiber to the organismal scale, yet the fundamental mechanism of muscle contraction lies at the molecular level. We therefore propose to extend the description to molecular scales using a ratchet-based model.
-
At the organismal level, energy fluxes during exertion can be assessed through measurements of mechanical power output and oxygen consumption. Using a swim tunnel available in the laboratory, we plan to compare two subpopulations of the small piranha Astyanax mexicanus, which display markedly distinct phenotypes: one active and fast, the other calm and slow. The objective is to characterize and compare their physiologies in light of derived thermodynamic observables.
| Astyanax mexicanus surface morphotype |
Astyanax mexicanus cave morphotype |
 |
 |
Living systems are characterized by a minimal energy consumption rate — the basal metabolism. This consumption is constrained by a single energy source that must simultaneously support use, maintenance, and structural synthesis, unlike engineered systems, which rely on distinct power sources for each function.
Here, we aim to explore and model the concept of basal metabolism in living systems. Specifically, we will investigate the ratio of energy fluxes between basal and active processes — such as reproduction, structure formation, or locomotion — in both photosynthetic organisms and animals, as well as the formation of local energy stocks that buffer demand. These analyses will allow for a quantitative comparison with engineered energy-conversion systems.
18 Dec 2024
Internship proposals for 2025
We look for intership students on the following thematics.
Integrated modelling of muscle contraction and extension
contacts:
eric.herbert@u-paris.fr , christophe.goupil@u-paris.fr
In this internship, we are interested in characterizing the relationship of force vs velocity response of the muscle, as described by the well-known phenomenological equation of Hill [Hill, 1938; Hill, 1970], established almost a century ago:
\(F(v) = \frac{c}{v+b} - a\)
The typical convex shape of \(F(v)\), due to its hyperbolic expression, and the small number of adjustable parameters have led to its success in recovering experimental contraction data accumulated since then.
But this description lacks a solid physical basis. Based on a description of an energy conversion machine, we were able to regain this expression where each of the parameters \(a\), \(b\), and \(c\) correspond to quantities that are thermodynamically founded and experimentally accessible. These involve a threshold current \(I_T\), the isometric force \(F_{iso}\), and the feedback resistance \(R_{fb}\) at the origin of the non-linearity. This description is valid both at the scale of the muscle and at that of the whole organism, as has been observed using data on oxygen respiration in horses [Herbert, 2020].
In the literature, studies looking at muscle contraction are frequent, but there is rarely a widening of the measurement range beyond \(F_{iso}\), i.e., exploring both muscle contraction and extension. Interestingly, however, Hill’s equation diverges when \(v = -b\), clearly indicating that this equation is not valid in the \(v < 0\) range. The description proposed in [Goupil, 2019] allows extension and contraction to be considered in the same framework. One working hypothesis is to make the feedback intensity depend on the deviation from zero speed. An example of a fit to experimental data is shown in Figure 1.
The work involves describing muscle extension and formalizing these descriptions so that they can be integrated into a model of the muscle as an energy conversion machine. We then derive the fundamental thermodynamic parameters that enable us to reconstruct the generalized Hill parameters, including extension with contraction. The work includes a literature review to explore the models proposed to describe the extension, as well as the establishment of an experimental dataset to test the models. A taste for modeling and thermodynamics is required. Experience of working with the Python language is preferable.
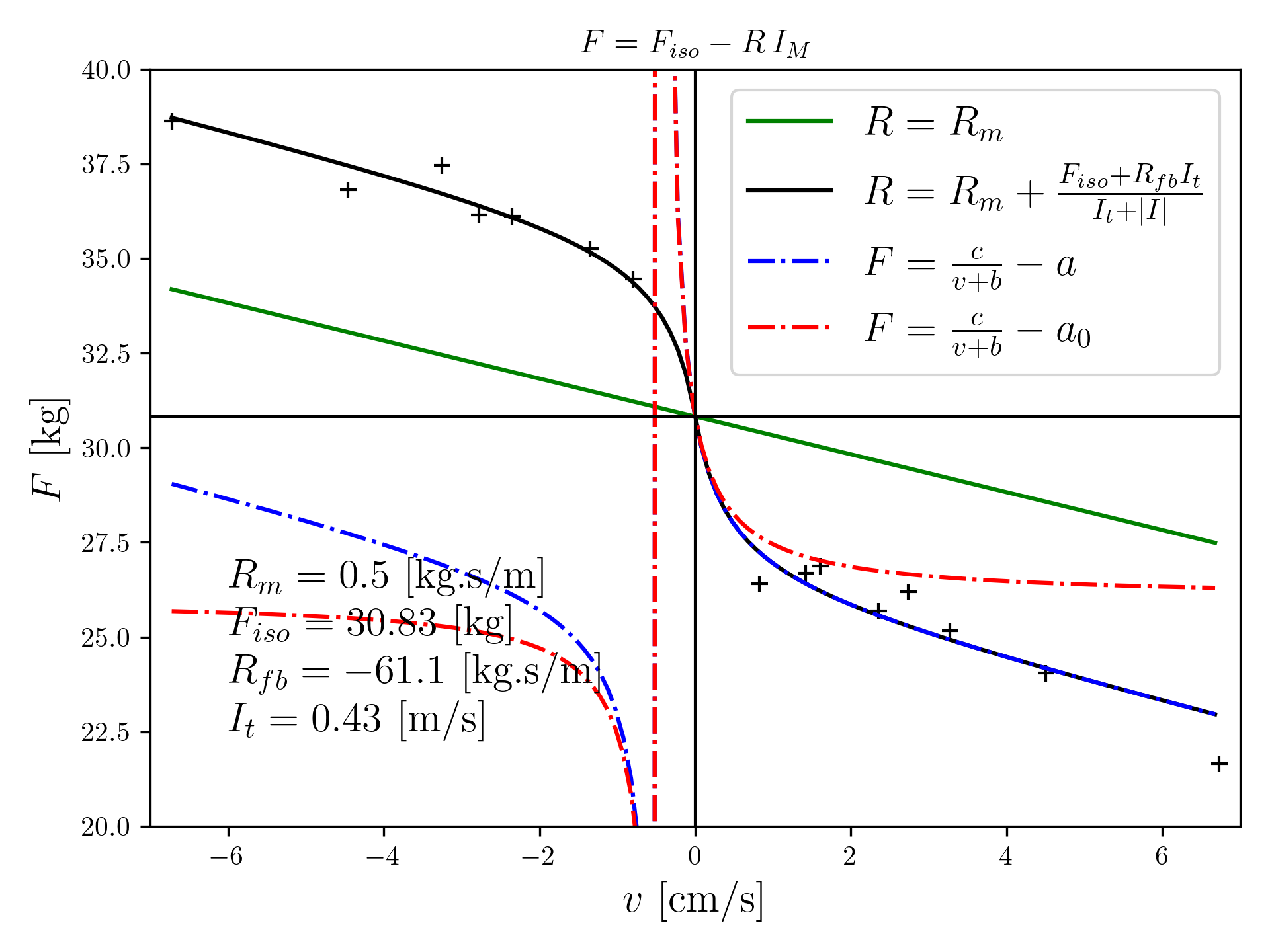
Figure 1: Fit of contraction velocity measurements and extension based on Vredenbergt data (\(\textbf{+}\)) with the proposed model (solid black line) and with Hill’s model including dissipation in parameter \(a\) (dashed blue line) and without dissipation (dashed red line).
Energy Modeling of Socio-Technical Structures
contacts:
eric.herbert@u-paris.fr , petros.chatzimpiros@u-paris.fr
Every human society relies on technology to organize the flows of matter and energy that pass through it. In industrial societies, technology is omnipresent through infrastructures and technologies across all sectors of activity. This is characterized by a high energy consumption required both for establishing these structures and for their operation. Generally, the energy consumption associated with the operation of these structures is more noticeable than that associated with their establishment, the latter being inherent to the industrial sector and largely invisible to users. The amount of energy embedded in these structures, also known as “embodied energy,” along with the rate (W) at which this energy is supplied—referred to as “embodied power”—depends on the processes as well as the type and complexity of the materials and structures involved.
The quantification of the embodied energy in objects and structures is typically addressed through “bottom-up” life cycle assessment (LCA) approaches. These involve reconstructing resource usage from an individual description of all stages and flows involved in a process. The main challenge lies in defining the scope of analysis, which should be as inclusive as possible but remains inevitably arbitrary to achieve an accurate reconstruction. Indeed, beyond the limitations related to setting a functional boundary in “space,” bottom-up approaches are typically static and struggle to account for the temporal dimension of development, in terms of the legacy of past infrastructures, technologies, and innovations in the production of the present.
In this work, we propose to focus on the embodied energy and power of structures using a top-down approach, starting from macroscopic consumption data to analyze the uses and renewal dynamics of structures. This top-down strategy relies on globally available energy balances over time [i.e., ref. 1], enabling analysis at the scale of the global socio-technical system. In this approach, and as a first approximation, the embodied energy of structures can be considered as the interannual sum of the inflow into the industrial sector, combined with a decay function to account for infrastructure wear and the resource investment needed for their renewal. This study can be conducted using published data from the recent past and can be leveraged to discuss energy transition scenarios.
In a second phase, and based on the established energy balances, we propose to focus on the competition between infrastructure use and production. Some uses are flexible and allow for storage when not in use, for example, a car that can charge at night, while other uses (e.g., a factory) are highly constrained, operating 24/7 and requiring a continuous, fully controllable energy source. To model these dynamics, we propose to construct a usage rate and mobilized power for each use, deriving the characteristics of an energy system compatible with the intermittency of renewable sources and the associated storage needs. This analysis will lead to the development of scenarios inspired by some recent work by the team [ref. 2].
[ref. 1] https://www.sankey-diagrams.com/global-energy-flows-2018-2050-dnvgl/
[ref. 2] https://doi.org/10.1371/journal.pone.0286242
Growth Dynamics of Podospora anserina Thallus
contact: eric.herbert@u-paris.fr
Master internship, at the interface of physics and biology, supervised by biologist and physicist, on the growth of branching networks in the case of the filamentous fungus Podospora anserina. We look for motivated students with a taste for numerical studies.
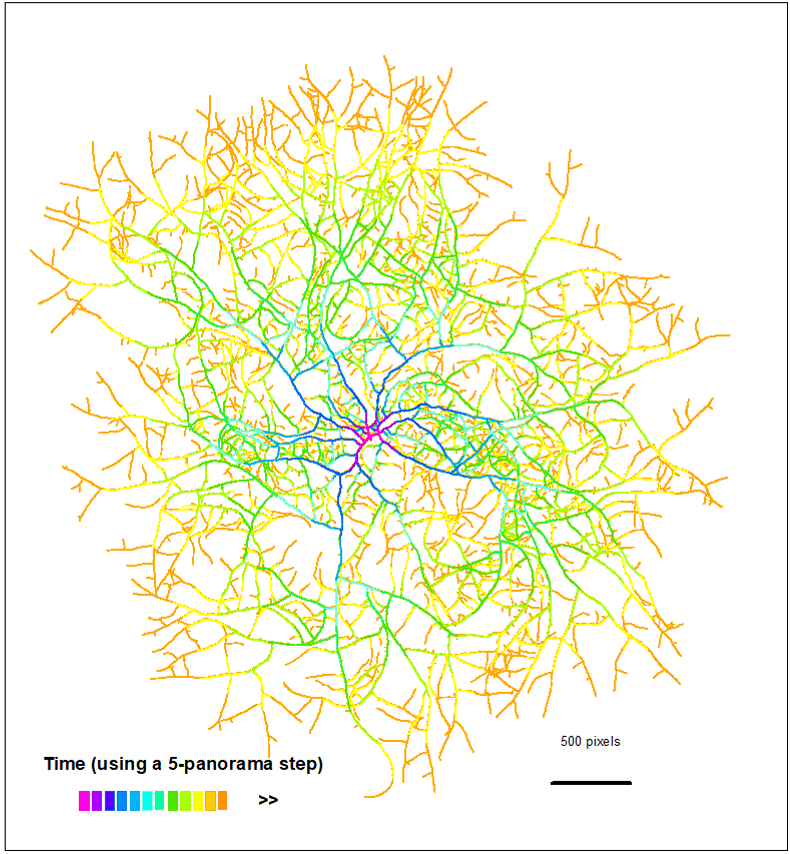
Hyphal network
The achievement of filamentous fungi in colonizing terrestrial ecosystems can be largely attributed to their flexible morphology, and more specifically to their ability to form an interconnected hyphal network, the mycelium, based upon some fundamental cellular processes, such as hyphal tip (or apex) growth, septation, hyphal orientation, branching, and fusion (also known as anastomosis).
Hyphal tip expansion is a highly polarized process, based upon secretory vesicles which are transported to the apical cell wall using a combination of microtubule and microfilaments, allowing a localized polar secretion of wall materials. Polarity is directly correlated to the morphology of the hypha via the growth velocity. The delivered secretory vesicles accumulate temporarily in an apical vesicle cluster, the spitzenkörper. Vesicle exocytosis at the apical membrane allows both the release of secretory enzymes and the expansion of apical membrane and cell wall.
P. anserina is autotrophic, meaning that its growth is not conditioned by any other organism, and is therefore a model for the growth of branching networks.
Internship
Initial work has made it possible to acquire a collection of growth images and to reconstruct the network in the form of a dynamic graph. Building on this work, the internship will focus on characterizing the network and its dynamics. At a local level, with interactions such as avoidance and attraction of hyphae/apex structures. At the global level, the spatial distribution of the material and the impact of hyphal overlap and fusion on the resilience of the network.
An experimental study could be envisaged to detect mergers in the network.
- Ledoux, et al. (2022). Prediction and Experimental Evidence of the Optimisation of the Angular Branching Process…. Scientific Reports.
- Ledoux, et al. (2023). Prediction and Experimental Evidence of Different Growth Phases…. Scientific Reports.
- Chassereau, et al. (2024). Full Identification of a Growing and Branching Network’s Spatio-Temporal Structures. arXiv, 2407.06824. Accepted in Biophysical Journal.
06 Nov 2023
Macroeconomic dynamics in a finite world based on thermodynamic potential
LIED —
Université Paris Cité, 35 rue H. Brion, 75013 Paris
Author
Eric Herbert ,
Gael Giraud,
Aurélie Louis Napoléon
and Christophe Goupil
contacts:
eric.herbert@u-paris.fr , christophe.goupil@u-paris.fr ,
————————————————————————
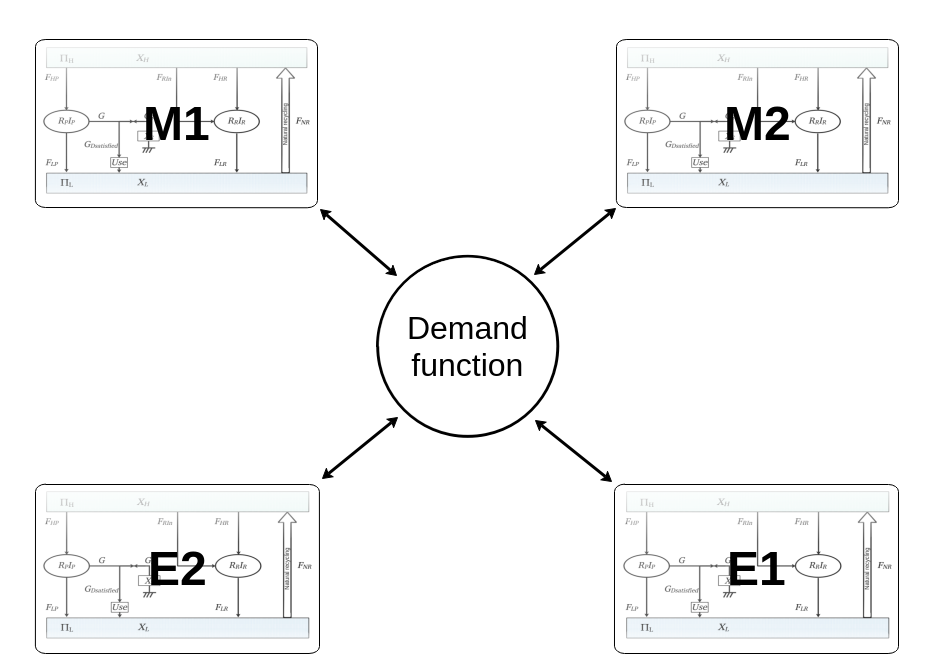 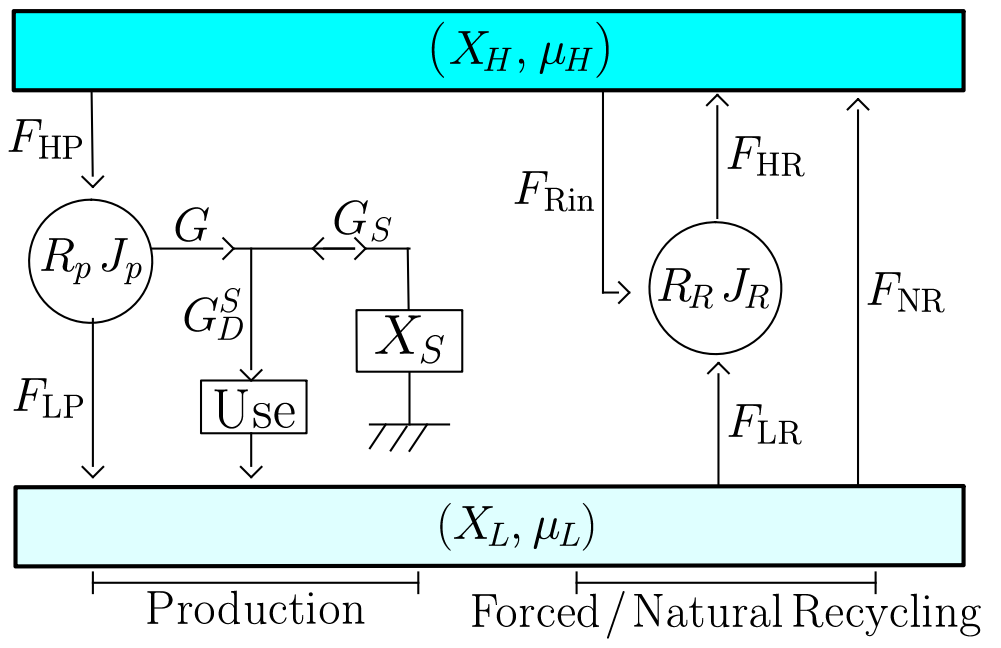 |
| Top, physical sheets with four sectors interconnected by a central kernel. |
| Bottom, global structure of a sheet of resource. Left part is the production area, middle part is forced recycling, and right part is natural recycling. |
In this work we are interested in the connection between economic spheres and physical resources. Rather than integrating thermodynamic formalism into economic modeling, we create a generic tool for describing the use of a resource as a function of its availability (the volume of its stock) and the intensity of its use, based on the concepts of quantity and quality.
Abstract of the paper
This paper presents a conceptual model describing the medium and long term co-evolution of natural and socio-economic subsystems of Earth. An economy is viewed as an out-of-equilibrium dissipative structure that can only be maintained with a flow of energy and matter. The distinctive approach emphasized here consists in capturing the economic impact of natural ecosystems’ depletion by human activities via a pinch of thermodynamic potentials. This viewpoint allows: (i) the full-blown integration of a limited quantity of primary resources into a non-linear macrodynamics that is stock-flow consistent both in terms of matter-energy and economic transactions; (ii) the inclusion of natural and forced recycling; (iii) the inclusion of a friction term which reflects the impossibility to produce (and recycle)goods and services without exuding energy and matter wastes, and (iv) the computation of the anthropically produced entropy as a function of metabolizing intensity and frictions. Analysis and numerical computations confirm the role played by intensity and frictions as key factors for sustainability by contrast with real gdp growth—as well as the interplay between resource scarcity, income inequality, and inflation. A more egalitarian society with moderate inflation turns out to be more sustainable than an unequal society with low inflation. Our approach is flexible enough to allow for various economic models to be embedded into our thermodynamic framework. Finally, we propose the open source EcoDyco software as a first complete realization implementing economic dynamics in a multi-resource environment.
To know more about it, see
Herbert, É., Giraud, G., Louis-Napoléon, A., & Goupil, C. (2023). Macroeconomic dynamics in a finite world based on thermodynamic potential. Sci. Rep., 13(18020), 1–27. doi
15 Oct 2023
Power Production in living systems: a biomimetic model of
optimisation constrained by resource management
LIED —
Université Paris Cité, 35 rue H. Brion, 75013 Paris
contacts:
eric.herbert@u-paris.fr ,
christophe.goupil@u-paris.fr ,
patrick.laurenti@u-paris.fr
  |
| Two morphotypes of the same species, Astyanax mexicanus. On the top the blind and depigmented cave morphotype, on the bottom the surface morphotype. |
Master internship
We propose a master internship at the interface of physics and biology, supervised by biologist and
physicist, to study the adaptation of the power production mechanism of
animals to the environment.
Power production
The power production mechanism, for example dedicated to locomotion, is a general and vital process
based in the animal world on the degradation of ATP molecules during the
Krebs cycle. However, this common process, far from freezing the
modalities of use and power production of living systems, adapts to the
specific environmental constraints encountered by each population.
More specifically, we are interested, in a biomimetic approach, in the
adaptive optimisation of energy conversion systems according to the
constraints imposed on access to resources.
To this end, we are developing a theoretical and experimental approach,
deriving the well-known formalism of non-equilibrium thermodynamics
to living systems and relying on the description of biological
mechanisms of metabolism, and in particular oxygen consumption. This
allows us to reconstruct the energy flows through the organism and to
characterise it quantitatively using generic parameters allowing
inter-individual comparison.
Although our approach has so far focused mainly on mammalian species (in
particular the horse, see ref below), the development of simple
metabolic characterisation tools allows us to consider broadening the
range of species studied. Following preliminary work carried out in the
laboratory, we have designed a device (swimming tube and sensors) to
record the consumption of dioxygen of actinopterygian fish. In order to
limit the effects due to genetic variability, we propose to compare
morphotypes of the same species. We have chosen Astyanax mexicanus, a
species in which there are two separate but interbreeding populations: a
surface morphotype, a predator with a very vivacious behaviour, and a
cavernicolous morphotype, a detritivore with a placid behaviour. In
addition, we propose to conduct a phylogenetic analysis that will allow
us to describe the evolution of biological processes that determine the
ability to produce and sustain effort in all vertebrate animals; and, in
particular, to characterise the evolution of mechanisms of adaptation to
effort during the transition from aquatic to terrestrial life in the
vertebrate lineage as a bioinspired model of adaptive transition.
To know more about it, see
Herbert et al. Thermodynamics of Animal Locomotion. Physical Review
Letters 125, 22 (2020): 228102.
https://doi.org/10.1103/PhysRevLett.125.228102
Goupil et al. Thermodynamics of metabolic energy conversion under muscle load, New J.
Phys., vol. 21 (2019),
https://iopscience.iop.org/article/10.1088/1367-2630/ab0223
[— Possibility of continuing to a PhD —]











