Dyco est une équipe du laboratoire LIED de l université de Paris qui s intéresse à la thermodynamique hors d équilibre et à ses conséquences sur le monde qui nous entoure
Dyco est une équipe du laboratoire LIED de l université de Paris qui s intéresse à la thermodynamique hors d équilibre et à ses conséquences sur le monde qui nous entoure
Cette page reprend le manuel du Code Ecodyco dont le code source est disponible ici.
Le modèle EcoDyco a été conçu sur la base de quatre constats :
Si le monde physique est modifié par l’application des lois de l’économie, il n’en demeure pas moins que son évolution est gouvernée pas des lois physiques.
Le monde physique est fini, ceci est vrai pour toutes les ressources matérielles et pour les ressources énergétiques fossiles.
Dans un monde fini, la définition d’une fonction de production doit prendre en compte l’état des ressources
L’intensité de prélèvement d’une ressource est un facteur majeur agissant sur le devenir de cette dernière.
Si l’économie n’est pas descriptible strictement par la thermodynamique, cette dernière peut lui fournir certaines catégories utiles, et, en particulier, la distinction entre quantité et qualité, elles-mêmes reliées au caractère intensif ou extensif des variables.
Ces trois constats fondent la structure et le fonctionnement du modèle EcoDyco:
Il est défini une fonction “demande”, qui remplace la traditionnelle fonction de production. En effet, en présence de ressources finies, il n’est pas possible d’affirmer, à priori, que la production sera effectivement satisfaite.
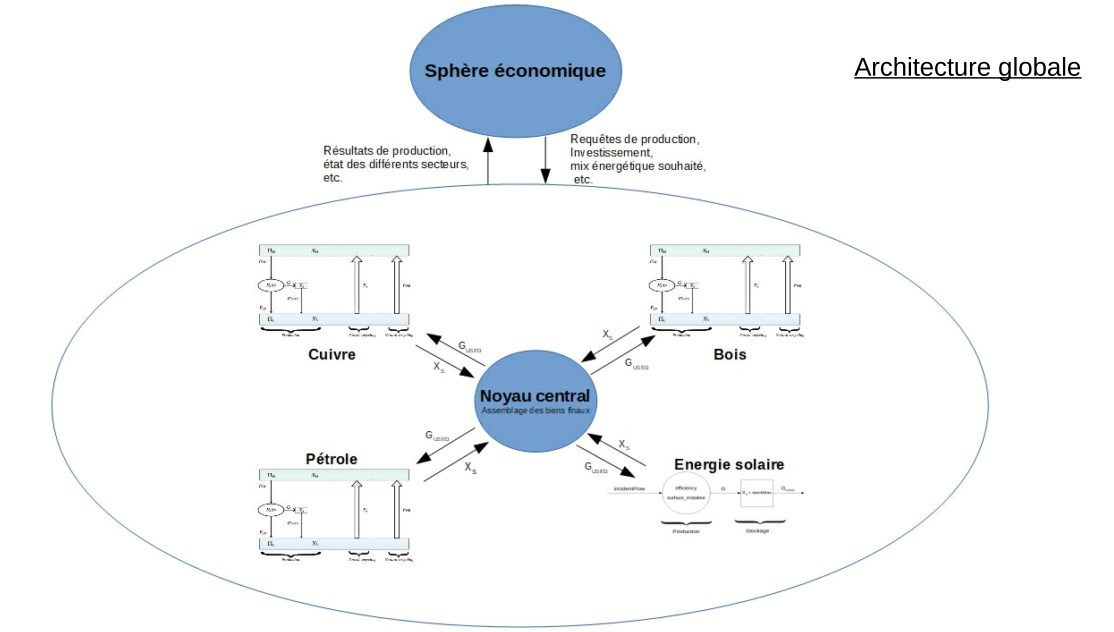
Les descriptions des sphères physique et économiques du modèle sont disjointes. Elles communiquent par l’intermédiaire des requêtes de production et la modification des capacités de l’outil de production via l’investissement et le progrès technique.
Chaque ressource est décrite dans un feuillet qui lui est propre. La collection de feuillets ainsi obtenue est la sphère physique. Chaque feuillet quantifie la fraction utilisable et la fraction utilisée de la ressource que l’on nommera déchet. La fraction utilisée ne peut être de nouveau utilisée qu’après recyclage.
Il est défini une intensité de fonctionnement de l’économie qui régit l’ensemble des feuillets physiques.
Aux quantités de ressources sont aussi associées des qualités, qui, à l’image des premiers et second principes de la thermodynamique, définissent, à quantités égales, la différence de qualité d’une ressource et son état de transformation, vers un produit ou vers un déchet.
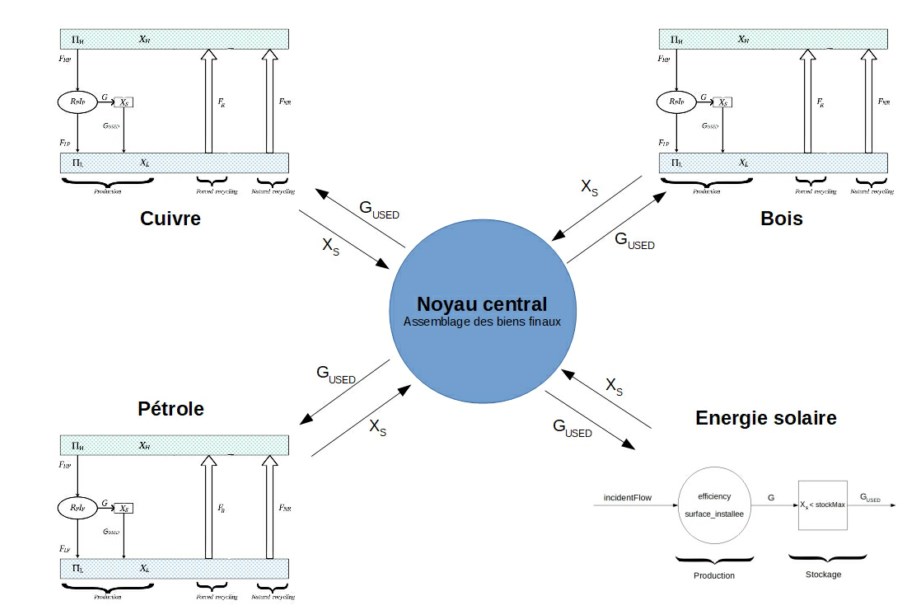
Le modèle EcoDyco est structuré en feuillets de type stock et de type flux, reliés au module économique (Fig. 1). Son architecture globale est la suivante:
Les feuillets de type stock sont destinés à la plupart des ressources, minières ou non, fossiles ou non, dont la quantité sur la planète est finie et de dispersion variable.
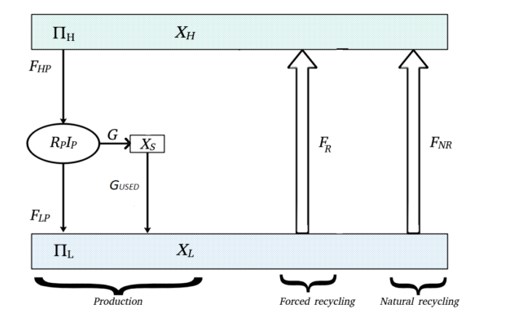
Sur un feuillet type (Fig. 2) on distingue une zone haute qui contient la ressource en quantité \(X_{H}\) et en qualité \(\Pi_{H}\) ainsi qu’une zone de ressource usagée en quantité \(X_{L}\) et en qualité \(\Pi_{L}\). Les flux de ressources de \(F_{HP}\) et de déchets \(F_{LP}\) constituent avec le flux de production \(G\) l’ensemble des flux de la ressource dans sa mise en oeuvre pour la production. La quantité de ressource mise en oeuvre de façon excédentaire constitue un stock \(X_{S}\). Le recyclage peut être naturel \(F_{NR},\) ou forcé, \(F_{R},\) selon des lois spécifiques. On nomme différence des potentiels la grandeur \(\Delta\Pi=\Pi_{H}-\Pi_{L}\).
Un feuillet stock est défini initialement par le jeu des paramètres limités dont la liste est donnée ci-dessous (Les valeurs sont données à titre d’exemple):
Son type: type : stock
Son nom: name : cuivre
Sa quantité totale: total stock : 500000
Son niveau de ressource initial: Xh_init : 500000
Son niveau de déchet initial: Xl_init : 0
Sa résistance de dissipation de production : Rp0 : 0.003
Ratio énergétique de recyclage (1 unité d’énergie pour recycler 1 unité de la ressource) : recyclingEnergyFlux : 1
Utilisable comme énergie (cas du pétrole) : isEnergy : False
Taux de recyclage naturel (r=0 : pas de recyclage) : r : 0
La description et l’utilisation de ces paramètres est décrite en détail dans les annexes de ce document. Une attention particulière est cependant portée sur \(R_{P}\)
La résistance de dissipation est un terme qui intervient, via l’intensité de production, sous la forme \(R_{P}I^{2}\). Ce terme indique la fraction de la ressource perdue, qui n’est pas utilisée pour la production de bien de consommation alors même que la ressource a été prélevée à la planète. \(R_{P}\) conduit à limiter la capacité d’un outil de production qui ne peut fonctionner sous intensité élevée. A un outil de production performant est associé une valeur faible pour \(R_{P}\). En tant que signifiant de l’outil de production \(R_{P}\) est donc directement lié au capital. Il s’en suit que \(R_{P}\) augmente naturellement au cours du temps sous l’effet de dégradation du capital. Pour la même raison, les efforts d’investissement conduisent à réduire \(R_{P}\). Il en va de même du progrès technique qui se traduit par une baisse brutale de \(R_{P}\) sous l’effet de la mise en oeuvre de ce progrès. Enfin, à progrès technique constant, la multiplication de site de production correspond à la mise en parallèle de plusieurs résistances \(R_{P}\) , ce qui conduit à réduire la résistance globale du même facteur, permettant ainsi de travailler à intensité supérieure puisque répartie sur les sites de production. Si une forte valeur de \(R_{P}\) traduit un outil de production incapable de fonctionner dans une économie à forte intensité de production, il est clair qu’une faible valeur de \(R_{P}\) n’est pas nécessairement une situation enviable au niveau écologique, au sens où la très grande capacité de l’outil de production est aussi un outil de prélèvement accru et massif de la ressource. La finitude associée au feuillet conduit alors à un pincement de production, sous l’effet de la raréfaction accélérée de la ressource.
On peut attribuer quatre effets principaux à la présence de \(R_{P}\):
Dégradation du capital qui se traduit à une augmentation de \(R_{P}\) avec les conséquences qui s’en suivent sur la qualité d’exploitation de la ressource.
Effet de l’innovation qui se traduit à une baisse de \(R_{P}\) avec les conséquences qui s’en suivent sur la quantité de prélèvement accrue de la ressource.
Augmentation de la capacité de production, à progrès constant, qui se traduit à une baisse de \(R_{P}\) global avec les conséquences qui s’en suivent sur la quantité de prélèvement accrue de la ressource.
Effet de l’investissement qui se traduit à une baisse de \(R_{P}\) avec les conséquences qui s’en suivent sur la quantité de prélèvement accrue de la ressource.
On notera aussi que quelle que soit la valeur de \(R_{P}\), il est observé une baisse des rendements de production pour des intensités de production au delà d’un certain seuil. En ce sens, \(R_{P}\) contribue au caractère Ricardien de l’apparition de rendements décroissants. Il importe de noter que la limitation des rendements trouve aussi son origine dans le mécanisme de raréfaction de la ressource qui est mis en évidence par la baisse de la différence de potentiel \(\Delta\Pi\). Cet effet de pincement conduit à mécaniquement réduire la production [1].
Les feuilles de type flux sont destinées aux ressources qui sont disponible sur la planète sous la forme d’un flux (Fig. 3). La plus usuelle étant naturellement l’énergie solaire.
Un feuillet flux est défini initialement par le jeu des paramètres limités dont la liste est donnée ci-dessous (Les valeurs sont données à titre d’exemple):
Son type : type : flow
Son nom name : energie solaire
Le flux incident : incidentFlow : 1e10
L’efficacité de conversion : eff_init : 0.15
La surface installée surface_installee : 1e-9
Utilisable comme énergie: isEnergy : True
Capacité maximale de stockage : stockMax_init : 50
Le noyau physique est le lieu de la réalisation des biens manufacturés. Le schéma de principe du fonctionnement de cette zone est donné dans la figure ci-dessous (Fig. 4).
Les “recettes” de fabrication des biens manufacturés sont indiquées dans la feuille world.txt. Le programme principal effectue automatiquement la réalisation en respect de ces “recettes”.
La zone économique est le lieu ou est codé le modèle économique sur lequel se fonde la simulation. Afin d’illustrer ce point, deux exemples de modèles sont données :
Goodwin
Solow
L’utilisateur avancé peut construire son propre modèle en suivant la structure générale d’une feuille économique. (voir Annexe A)
Vous devez avoir dans un dossier:
les scripts python :
le fichier PhysicalWorld.py
un fichier décrivant votre sphère économique. Dans ce manuel nous nous appuierons sur le modèle de Goodwin, décrit ans le fichier Goodwin.py.
le fichier main.py
autant de fichiers de paramétrage que nécessaire[2]:
world.txt (indispensable)
petrole.txt si vous avez une feuille pétrole
cuivre.txt si vous avez une feuille cuivre
Il suffit d’exécuter le fichier main.py.On modifie dans main.py le pas de temps deltat, et l’étendue temporelle de la simulation tmax.
Pour modifier les paramètres physiques (paramètres des cellules, et paramètres globaux de la sphère physique), il faut modifier les fichiers .txt correspondant.
Paramétrage de la nouvelle cellule:
pour créer une cellule stock, prendre le template StockCell.txt, rentrer les paramètres souhaités, et enregistrer sous le nom de la ressource (ex : cuivre.txt)
pour créer une cellule flux, faire de même avec le template FlowCell.txt
ensuite, ajouter dans world.txt votre nouvelle cellule dans le tableau cells.
enfin, rajouter la colonne correspondante a recipeMatrix dans world.txt
Supprimer la cellule dans le tableau cells de world.txt
Supprimer la colonne correspondante de recipeMatrix dans world.txt
Les paramètres globaux et valeurs initiales des variables globales de la sphère physique sont stockés dans les fichiers world.txt.
Les paramètres et valeurs initiales des variables des feuilles sont stockés dans les fichiers nom_de_la_feuille.txt.
Ne pas oublier d’enregistrer le fichier .txt apres modification d’une valeur[3].
Le message " world successfully created " s’affiche dans la
console lorsque le modèle a été initialisé.
L’exemple ci-dessous illustre la paramétrisation dans le cas d’un modèle Goodwin (Fig. 5).
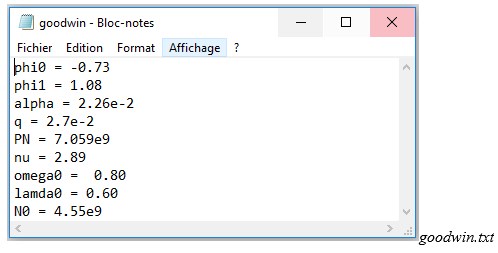
\(phi0\) et \(phi1\) sont les paramètres de la courbe de Philipps
\(alpha\) est le taux de croissance de la productivité du travail
\(q\) est le taux de croissance de la population
\(P_{N}\) est la valeur maximale de la population (le taux de croissance réel de la population N est \(q\ast(1-N/P_{N}))\)
\(nu\) est la productivité du capital
\(omega0,lambda0\) et \(N_{0}\) sont les valeurs initiales du wageshare, employment rate et de la population
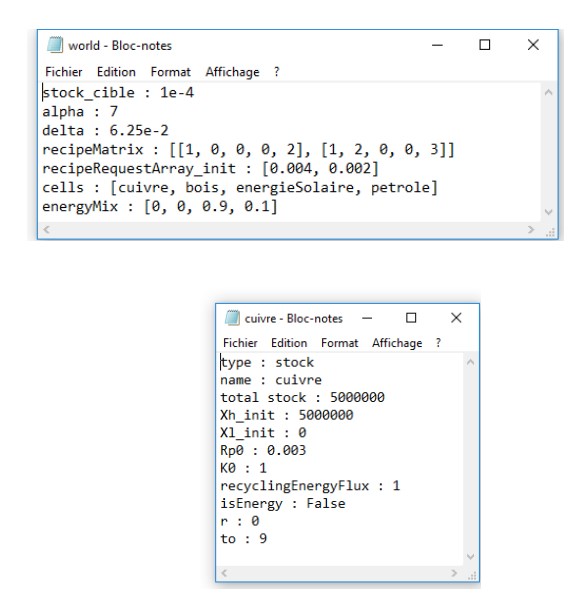
On se propose d’illustrer le fonctionnement de EcoDyco par une étude de cas (Fig. 6) basée sur
4 ressources : cuivre, bois, pétrole, solaire
3 recettes:
1 cuivre + 2 énergie => bien 0
1 cuivre + 2 bois + 3 énergie => bien 1
1 énergie => bien 3 (recyclage cuivre)
1 Mix énergétique cible : 90% solaire, 10% pétrole
Dans le fichier principal main.py, on effectue
le choix du fichier Solow.py comme modèle économique
paramétré par le fichier solow.txt (Fig. 7).
le choix du pas de temps et de la durée de la simulation
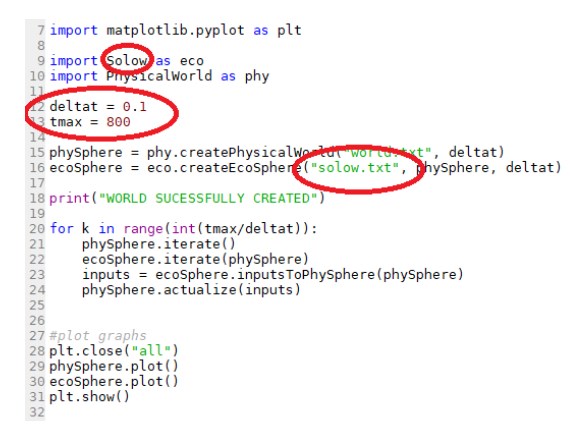
Dans le fichier du modèle économique on spécifie ses paramètres. (ici Solow.txt) (Fig. 8).
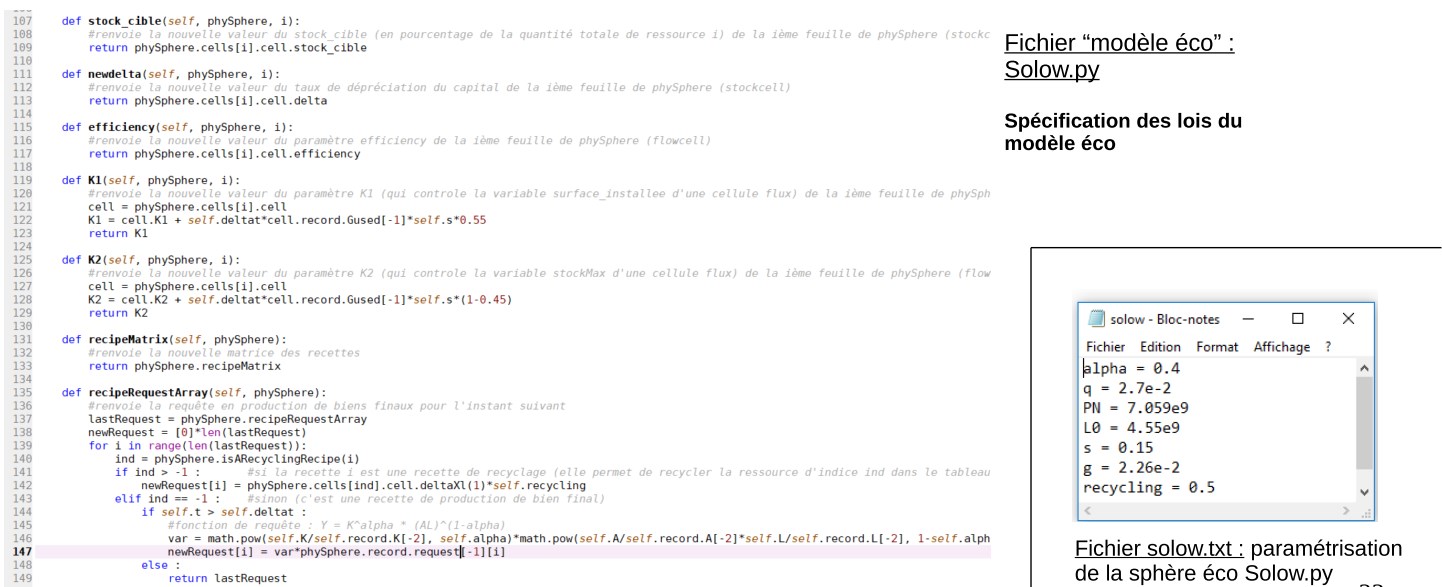
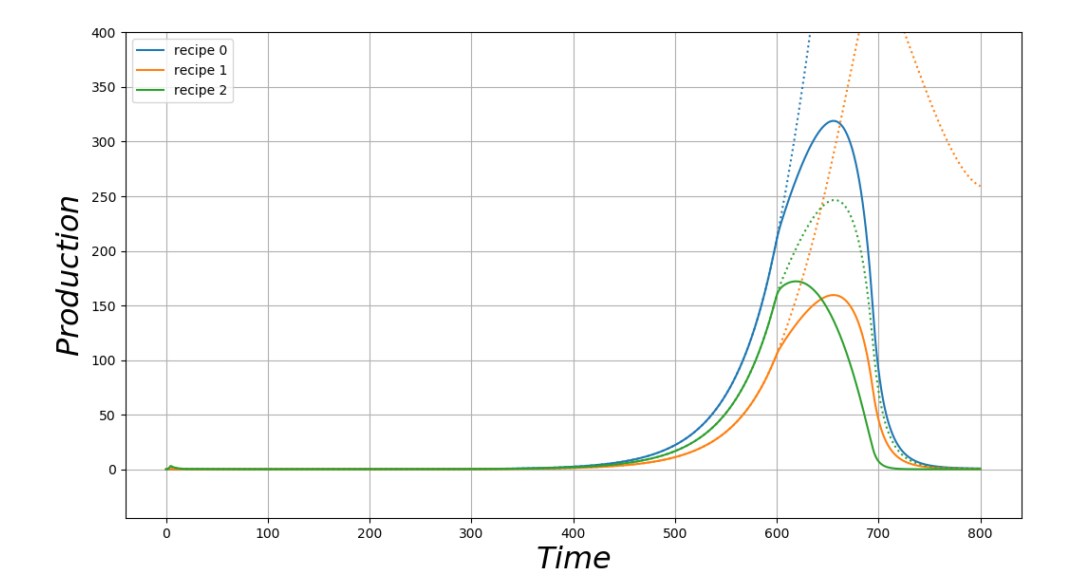
Le lancement de la simulation via le module main.py conduit au résultat suivant pour la production et l’énergie(Fig. 9) (Fig. 10):
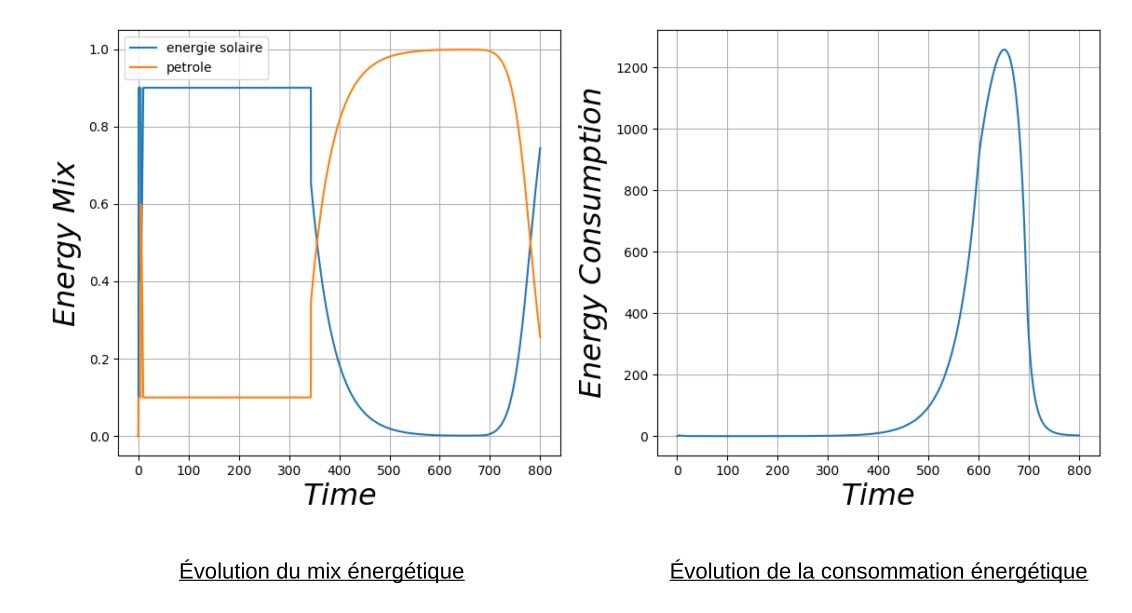
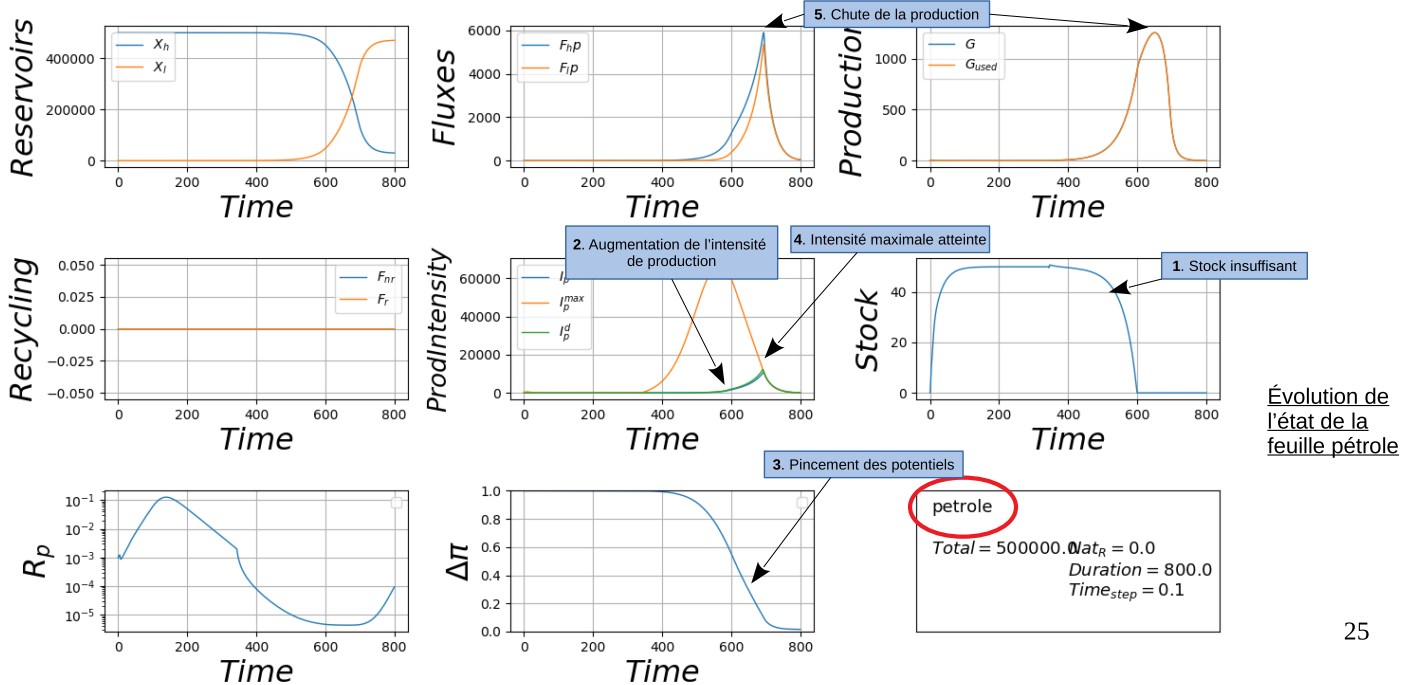
Toutes les informations relatives à chacun des feuillets étant enregistrées, il est possible de suivre les paramètres à volonté, par exemple ici pour le pétrole (Fig. 11):
Si l’on souhaite utiliser un modèle économique différent pour la sphère économique, parmi les modèles disponibles, il faut effectuer les modifications suivantes dans le fichier main.py
Ligne 9 : Spécifier le nom du fichier .py décrivant la sphère éco (ici Goodwin.py)
Ligne 17-18 : créer une instance de la sphère éco avec un appel de la fonction eco.createEcosphère() - vérifier que les arguments pris par cette fonction correspondent bien aux arguments demandés par la fonction createEcoSphere de votre fichier EcoModel.py (ici Goodwin.py)
Ligne 36: De même, vérifier les arguments pris par la fonction ecoSphere.inv()
Ligne 40: De même, vérifier les arguments pris par la fonction ecoSphere.iterate()
Ligne 42: De même, vérifier les arguments pris par la fonction ecoSphere.newProdRequest()
Il est possible d’insérer n’importe quel modèles économique au programme DyCoEco. Si vous souhaitez en écrire un vous même pour l’ajouter a la bibliothèque des modèles disponibles, vous devez respecter la structure suivante dans votre script :
Le fichier .py doit contenir :
une classe EcoSphere contenant :
un constructeur __init__
une fonction iterate
une fonction inv
une fonction newProdRequest
une fonction plot
Un exemple de modèle économique (trivial) respectant cette structure est donné ci-dessous (ecoVide.py).Le rôle des fonctions citées ci-dessus est également détaillé
Les ressources de type “ stock ” sont supposés être en quantité globale constante. Une unité de ressource “ stock ” peut se trouver dans trois états différents.
Elle peut etre “disponible ”, c’est à dire pouvant être extraite par l’appareil de production en vue d’une transformation ultérieure (ressources valorisables). Elle peut également avoir déjà été extraite, et être en attente de transformation en bien final. Enfin, elle peut etre usagée, c’est à dire que la sphère économique est incapable de la valoriser.
On définit trois réservoirs contenant les ressources dans chacun de ces trois états : un réservoir haut pour la fraction disponible de la ressource, un stock pour la fraction de la ressource en attente de transformation ultérieure, et un réservoir bas pour la fraction usagée de la ressource.
On note \(X_{H},X_{S}\) et \(X_{L}\) les quantités correspondantes, et \(X_{T}\) la quantité totale de ressource.
Ainsi, on a a chaque instant :
\[X_{H}+X_{S}+X_{L}=X_{T}\]Ensuite, on comptabilise strictement les mouvements entre ces trois réservoirs.
L’extraction de la ressource est le processus permettant de convertir une unité de ressource “ disponible” en une unité de ressource “ en attente ”. Ce processus n’a le plus souvent pas une efficacité de 100%: une fraction des ressources disponibles extraites est immédiatement transformée en déchets. Ce processus est analogue à la production de travail par un moteur thermique : on produit, a partir de la différence de température entre deux thermostats, une certaine quantité de travail utile W, tandis qu’une part de l’énergie provenant de la source chaude \(Q_{C}\) est dissipée sous forme de chaleur \(Q_{F}\).
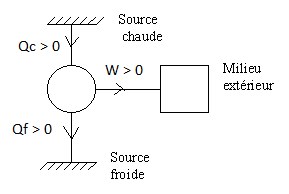
Ici, la source chaude devient le réservoir de ressource “ disponible ”, la source froide le réservoir de ressource “ usagée ”, et le travail produit est stocké.
On note \(F_{HP}\) le flux provenant du réservoir haut, \(F_{LP}\) le flux en direction du réservoir bas, et \(G\) le flux de ressources en direction du stock. Ainsi,
\[G=F_{HP}-F_{LP}\]Les ressources dans le stock \(X_{S}\) sont ensuite transformées en bien final. Apres utilisation, la ressource devient déchet. On note \(G_{USED}\) ce flux entre le stock et le réservoir bas.
L’ensemble de ces flux définit la zone de production. Une unité de ressource usagée peut parfois etre recyclée. Ce recyclage peut etre naturel, ou la conséquence d’une activité humaine. On note \(F_{NR}\) le flux de recyclage naturel, et \(F_{R}\) le flux de recyclage humain.
Au fur et à mesure que l’on exploite la ressource disponible, sa qualité diminue, car on exploite la ressource de bonne qualité en premier. Or, la qualité de la ressource a un impact sur l’effort a fournir pour l’extraire. Par exemple, pour une ressource minière, il faut fournir un effort plus important (l’intensité de production) apres trois années d’exploitation de la mine qu’au début de l’exploitation pour en extraire le même flux. En effet, la qualité de la ressource (sa concentration notamment) s’est dégradée. La notion de qualité est donc essentielle dans le processus d’extraction. La thermodynamique établit bien cette distinction entre quantité et qualité. On introduit donc ici une notion de thermodynamique, le potentiel. C’est une variable intensive. Les ressources dans le réservoir haut sont a un certain niveau de potentiel, \(\Pi_{H}\). \(\Pi_{H}\) diminue au fur et a mesure de l’extraction de la ressource du stock haut. \(\Pi_{H}\) est donc une fonction croissante de \(X_{H}\).
On a : \(F_{HP}=\Pi_{H}I_{P}\) et: \(\Pi_{H}=f_{1}(X_{H})\)
Les déchets dans le réservoir bas sont une pollution, qui a une rétroaction négative sur la production. Cette rétroaction se manifeste par l’augmentation du potentiel du réservoir bas, \(\Pi_{L}\).
On a : \(F_{LP}=\Pi_{L}I_{P}\)
\[Pi_{L}=f_{2}(X_{L})\]Le choix des fonctions \(f_{1}\)et \(f_{2}\)est important si l’on souhaite obtenir des résultats quantitatifs avec le modèles. Si l’on ne souhaite que des résultats qualitatifs, on peut se contenter de décrire la forme que devraient avoir ces fonctions (croissante ou décroissante, concave ou convexe, etc…)\(_{.}\) Dans la suite, on prendra pour \(f_{1}\) une fonction croissante et convexe, telle que \(f_{1}(X_{H}=0)=0,5\) et \(f_{1}(X_{H}=X_{T})=1\). On prendra pour \(f_{2}\) une fonction croissante et concave, telle que \(f_{1}(X_{L}=0)=0etf_{1}(X_{L}=X_{T})=0,5\).
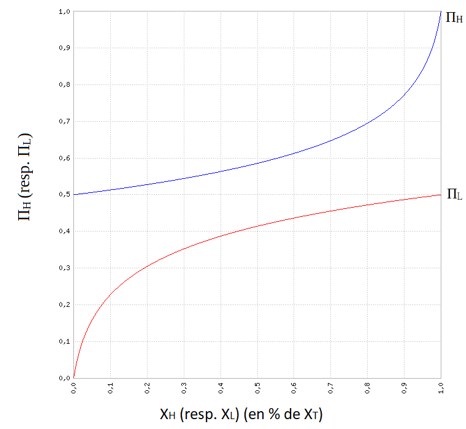
Lorsque toute la ressource est dans le réservoir haut, \(\Pi_{H}=1\) et \(\Pi _{L}=0\). La différence de potentiel \(\Delta\Pi\) est maximale. Lorsque toute la ressource est dans le réservoir bas, \(\Pi_{H}=\Pi_{L}=0,5\). La différence de potentiel est nulle, et la production est impossible. L’activité économique sans recyclage entraîne le passage de ressources entre le réservoir haut et le réservoir bas, donc une diminution de \(\Delta\Pi\). Autrement dit, l’activité économique sans recyclage entraîne une diminution de la capacité ultérieure à produire.
Finalement, on a introduit des variables extensives pour décrire la quantité \((X_{H},X_{L},X_{S},X_{T})\), et des variables intensives pour décrire la qualité de la ressource \((\Pi_{H},\Pi_{L})\)
Le temps joue un rôle dans le processus d’extraction de la ressource. Plus précisément, produire a une intensité tres élevée n’est pas équivalent a produire a faible intensité. A faible intensité, le rendement du processus est meilleur, mais le flux produit \(G\) est moins important. A intensité élevée, \(G\) est plus élevé mais le rendement est dégradé.
On introduit donc une résistance \(R_{P}\). On a alors un terme de friction \(R_{P}I_{P}^{2}\), et \(F_{LP}\) ce qui donne :\(F_{LP}=\Pi_{L}I_{P}+R_{P}I_{P}^{2}\)
En résumé, les équations décrivant l’extraction sont:
\[F_{HP}=\Pi_{H}I_{P}\] \[F_{LP}=\Pi_{L}I_{P}+R_{P}I_{P}^{2}\]\(G=F_{HP}-F_{LP}=\Delta\Pi I_{P}-R_{P}I_{P}^{2}\)
Le flux extrait $G$ est donc fonction de la différence de potentiels, de l’intensité de production, et de la résistance. Supposons \(\Delta\Pi\) et \(R_{P}\) fixés. $G$ est alors une fonction parabolique de \(I_{P}\).
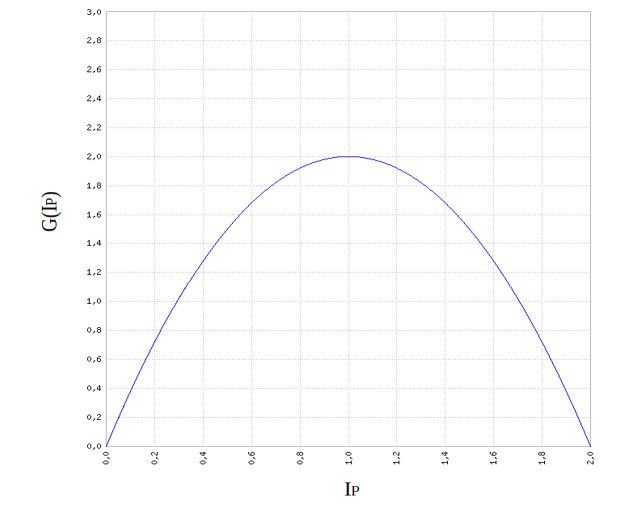
Le terme de friction quadratique entraîne qu’au delà d’un certain seuil \((I_{P}=\Delta\Pi/2R_{P})\), augmenter encore l’intensité de production diminue en fait le flux extrait \(G\).
Lorsque l’on souhaite atteindre un certain niveau de flux d’extraction G, il y a donc zéro, une, ou deux intensités de production possible. S’il y en a deux, on choisira systématiquement la plus basse. Ainsi, la valeur \((I_{P}=\Delta \Pi/2R_{P})\), qui permet d’atteindre le flux d’extraction maximal est aussi la valeur maximale de \(I_{P}\). On notera cette valeur \(I_{p}^{max}\).
De plus, il est possible que le niveau de flux d’extraction G requis ne soit pas atteignable, selon le couple \((\Delta\Pi,R_{P})\). La valeur maximale de G est \(G^{max}=\Delta\Pi^{2}/4R_{P}\)
Il est donc possible que la sphère économique fixe une requête de production qui ne puisse pas etre satisfaite. La possibilité de ce défaut de production constitue le coeur du modèle: c’est là que se manifeste la rétroaction de la sphère physique sur l’activité économique. Un tel défaut de production est favorisé par :
Une requête de production élevée
Une différence de potentiel faible (on parle de pincement des potentiels)
Une résistance élevée
De plus, l’efficacité du processus d’extraction, définie par \(\eta=G/F_{HP}\), vaut:\(\eta=1-\Pi_{L}/\Pi_{H}-R_{P}I_{P}^{2}/F_{HP}\)
A intensité nulle, on retrouve une expression analogue au rendement de Carnot. Ensuite, l’efficacité diminue a mesure que l’intensité augmente. Il s’agit donc de trouver un compromis entre efficacité \(\eta\) et flux extrait \(G\). Enfin, le processus d’extraction possède une certaine inertie. Si l’on est capable instantanément de calculer l’intensité de production idéale permettant de répondre a la requête de la sphère économique, l’intensité de production réelle s’ajuste avec un certain retard. On définit une intensité de production demandée \(I_{P}^{D}\). Le retard est caractérisé par un temps caractéristique de réponse de production \(\tau\).
On a alors : \(dI_{P}/dt+\tau I_{P}=I_{P}^{D}\)
Remarquons que cela permet de donner une signification physique au temps du modèle. Désormais, la période de \(t=10\) à \(t=20\) dans le modèles, soit \(\Delta t=10\), peut etre comparé aux temps de réaction des feuilles, qui eux ont une signification physique.
Le flux de recyclage naturel est donné par la relation:
\[F_{NR}=r( 1-\exp(\frac{X_{L}}{0.5X_{T}})\]ou r est le taux de régénération naturel.
Parfois, un processus permettant de recycler une ressource est connu et maîtrisé par l’Homme. On parle de recyclage “ humain ”, par opposition au recyclage naturel. Ces processus de recyclage humain sont des activités économiques à part entière, et le recyclage d’une unité de ressource nécessite un apport d’énergie (et de matière). Dans l’état actuel du modèle, on suppose que recycler “ humainement ” une unité de ressource nécessite un apport de x unités d’énergie. La valeur x correspond au paramètre recyclingEnergy, spécifique a chaque feuillet[4]. On a introduit ici une notion de finalité de la production : la combinaison de certaines ressources permet de produire un bien (ici un service) : le recyclage d’une autre ressource. Les notions de bien final et de recettes de production formalisent cette idée. Dans le modèle, elles sont implémentées au niveau de la sphère physique, au-dessus des différentes feuilles ressources. On parle de noyau central, englobant toutes les feuilles ressources.
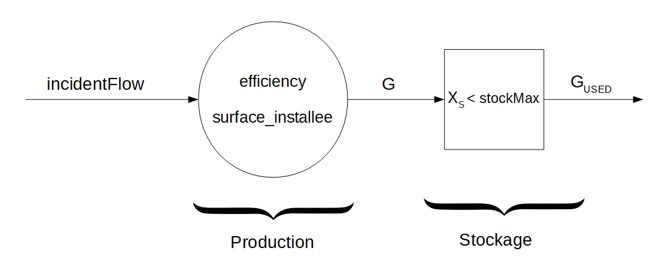
Un feuillet de type “ flux ” est défini par un flux incident \(P_{i}\) (intégré sur toute la surface de la Terre), et un appareil de production caractérisé par un rendement \(\eta\) et une surface installée \(S\) (en pourcentage de la surface terrestre). L’appareil de production permet l’extraction de cette ressource, c’est a dire sa mise à disposition pour une transformation ultérieure.
Le flux extrait est :$$G=\eta P_{i}S$
Ce flux peut etre immédiatement utilisé, ou stocké en attente d’utilisation. La capacité de stockage est définie par le paramètre \(stock_{Max}\).
L’utilisation de la ressource correspond à un flux sortant du stock, noté \(G_{USED}\).
Ainsi, le stock \(X_{S}\) vérifie : \(\Delta X_{S}=G-G_{USED}<X_{S}<stock_{Max}\)
Le noyau central est la zone d’assemblage des ressources précédemment extraites pour formation des biens finaux. Les recettes de production définissent les ingrédients et quantités nécessaire a la formation d’une unité d’un bien final. Par exemple, on peut définir le bien final “ barque ” avec la recette :
5 bois + 3 énergie = 1 barque
L’ensemble des coefficients des recettes définit une matrice des recettes, dont les colonnes représentent les ressources et les lignes les biens finaux.
On suppose que les requêtes de la sphère économique s’expriment en unité de bien final. Les requêtes de production de chaque ressource se déduisent grâce aux coefficients des recettes.
Comme les recettes définissent des proportions entre les ressources, les productions de chaque ressources doivent s’ajuster les unes aux autres en permanence. Par exemple, en reprenant l’exemple précédent, si la production de bois chute, la production d’énergie doit diminuer d’autant : il ne sert à rien de continuer à bruler du pétrole si l’on n’utilise pas l’énergie produite.
La mise en place de stratégies permettant d’obtenir ce résultat a fait l’objet de plusieurs tentatives.
Dans la stratégie retenue on fixe à chaque feuillet un objectif de stock à atteindre. Ensuite, l’intensité de production de chaque feuille s’ajuste afin de faire converger la valeur du stock vers le stock cible, et de l’y maintenir. Plus précisément, la variation de l’intensité de production demandée \(\Delta I_{P}^{D}\) est donnée par l’équation :\(\Delta I_{P}^{D}=a(X_{S}-X_{S}^{CIBLE})+b(dX_{S}/dt-0)\)
On souhaite que \(X_{S}\) converge vers \(X_{S}^{CIBLE}\), et \(dX_{S}/dt\) vers 0 : \(\Delta I_{P}^{D}\) est donc fonction des écarts \(X_{S}-X_{S}^{CIBLE}\) et \(dX_{S}/dt-0\). A l’équilibre, \(\Delta I_{P}^{D}\)est nulle.
\(a\) et \(b\) sont des paramètres définissant la préférence relative entre les deux objectifs (\(X_{S}=X_{S}^{CIBLE}\) et \(dX_{S}/dt=0\)).
Dans cette stratégie, chaque feuillet fixe de manière autonome son intensité de production. On décrit ainsi une situation où chaque secteur de production auto-régule sa production en fonction de ce qu’il vend. L’introduction de la notion de recette permet également de faire apparaître l’idée qu’on ne peut pas produire de bien final sans énergie. En effet, la recette de production indique la quantité d’énergie nécessaire à la réalisation d’une unité de bien final. Si cette quantité n’est pas disponible, on ne produit pas de bien final, c’est à dire qu’on “ n’utilise ” pas la ressource qui a été extraite pour, une fois associée à de l’énergie, être transformée en un bien final. Face à cette non utilisation, et afin de ne pas constituer de stock trop important, la feuille ressource va de manière autonome diminuer son intensité de production. Ainsi, l’introduction de la notion de recette permet de rétroagir sur l’extraction de toutes les ressources en cas de manque d’énergie : on ne peut rien produire sans énergie. Ce raisonnement est également valable en cas de défaut de production d’une ressource autre qu’énergétique.
Ainsi, chaque feuille extrait à chaque pas de temps une certaine quantité de ressources. Elle s’ajoute à la quantité de ressources “en stock” \(X_{S}\) disponible pour transformation ultérieure. La détermination du nombre d’unités de biens finaux produits est fonction:
des quantités de ressources ”en stock”
des requêtes de production de bien final provenant de la sphère économique
de la matrice des recettes
Il s’agit donc d’allouer les ressources aux différentes recettes de production de biens finaux. Il existe différentes méthodes d’allocations possibles. Par exemple : prioriser absolument la production du bien final \(n^{o}1\) au détriment de tous les autres, ou, a l’inverse, produire des biens finaux en quantité égale sans tenir compte des requêtes de production, ou encore, produire des biens finaux en respectant au maximum les proportions définies par les requêtes de production émanant de la sphère économique.
Cette derniere stratégie semble la plus naturelle. Cela signifie que l’on considère que les requêtes de production de biens finaux correspondent à la demande du marché, et que l’on souhaiterait satisfaire toutes les demandes simultanément, mais qu’en cas d’impossibilité, on répartit le défaut de production entre tous les biens finaux utilisant cette ressources. L’algorithme renvoie les allocations des ressources à la production des différents biens finaux.
Lorsque la production d’un bien requiert de l’énergie, elle peut être réalisée quelle que soit la provenance de cette énergie: pétrole, charbon, gaz, nucléaire, solaire, etc. Il faut donc spécifier dans la recette le besoin en énergie, et non pas le besoin en chaque ressource énergétique. Cela implique qu’il faut indiquer, parmi les feuilles, lesquelles sont des ressources énergétiques. On utilise ensuite ces ressources pour répondre au besoin en énergie. On définit ainsi un mix énergétique effectif.
De plus, on définit lors du lancement d’une simulation un mix énergétique souhaité, que l’on va chercher a satisfaire lorsque c’est possible. Le mix énergétique effectif peut etre différent du mix énergétique souhaité, par exemple si une ressource énergétique vient a manquer.
Finalement, la sphère physique décrit l’évolution de l’état de la ressource au cours du temps, et comptabilise les flux de matiere et d’énergie engendrés par la production de biens et par le recyclage. Mais les niveaux de production et de recyclage souhaités sont des décisions humaines, auxquels la sphère physique ne fait que répondre. Les lois décrivant l’évolution de ces requêtes sont décrites dans la sphère économique.
Le rôle de la sphère économique est de spécifier l’évolution de l’ensemble des variables économiques. En particulier, elle indique a la sphère physique :
des requêtes de production pour chaque bien final
une requête de recyclage “ humain ” pour chaque ressource concernée
le mix énergétique souhaité
l’investissement, pour chaque secteur (feuille), qui permet d’augmenter le capital. Le capital est directement relié a la résistance R\(_{P}\)des feuilles “ stock ”, et aux variables surface installée S et stockMax des feuilles “ flux ”
le niveau de stock cible pour les feuilles de type “ stock ”
On spécifie dans la sphère économique les lois décrivant le progrès technique éventuel. Le progrès technique correspond ici a la diminution des quantités de ressources nécessaires à la production d’une unité de bien final. C’est donc un gain d’efficacité: il faut moins d’énergie pour usiner une pièce, ou moins d’aluminium pour produire une canette. Dans le modèle, cela correspond à la diminution des coefficients de la matrice des recettes. La découverte d’un nouveau matériau, ou le développement d’une technologie permettant de substituer un matériau par un autre constitue une autre forme de progrès technologique[6]. Dans la suite du développement du modèle, la notion de substitution pourra etre représentée par une modification des recettes de production. Remarquons bien que la sphère économique n’adresse que des “requêtes de production” à la sphère physique. Cela implique que ces requêtes peuvent être, ou non, satisfaite, par exemple en cas de pincement des potentiels décrivant l’état de la ressource. Ce point est capital, puisqu’ il implique la possibilité d’ une rétroaction de la sphère physique sur la sphère économique. L’ ensemble de lois décrivant l’évolution de ces variables constitue la sphère économique. L’ architecture du code du modèles rends ces lois accessibles et modifiables facilement. Dans la démarche du projet, l’ utilisateur est encouragé à tester divers paramètres, lois et modèles macroéconomiques. Une bibliothèque d’ exemples de telles lois commence à être constituée. En particulier, on peut utiliser comme requête de production les fonctions de production de modèles macroéconomiques, et comme investissement celui décrit par ces mêmes modèles.
Il existe plusieurs niveaux d’ utilisation du modèle:
le premier niveau consiste a faire tourner le modèle en utilisant dans la sphère économiques des lois déjà pré-écrites et en faisant uniquement varier les paramètres (nombre de ressources, leurs caractéristiques, choix du mix énergétique, recyclage demandé, etc). Par exemple, a faire varier le taux de croissance de la productivité du travail dans un modèle de Solow.
Le second niveau consiste a tester diverses lois (et modèles macro-économiques) parmi la bibliothèque de lois disponibles. Cela permet d’ observer la sensibilité de la sphère physique au choix de ces lois.
Enfin, l’ utilisateur maîtrisant déjà bien le modèle est invité a proposer de nouvelles lois lui-même, afin d’ enrichir la bibliotheque. Une loi peut correspondre par exemple a la fonction de production d’ un modèle macroéconomique, a une hypothese concernant le rythme du progres technique, ou a l’ introduction d’ une rétroaction entre l’état des ressources et le mix énergétique souhaité.
Un exemple de sphère économique basée sur le modèle de Solow
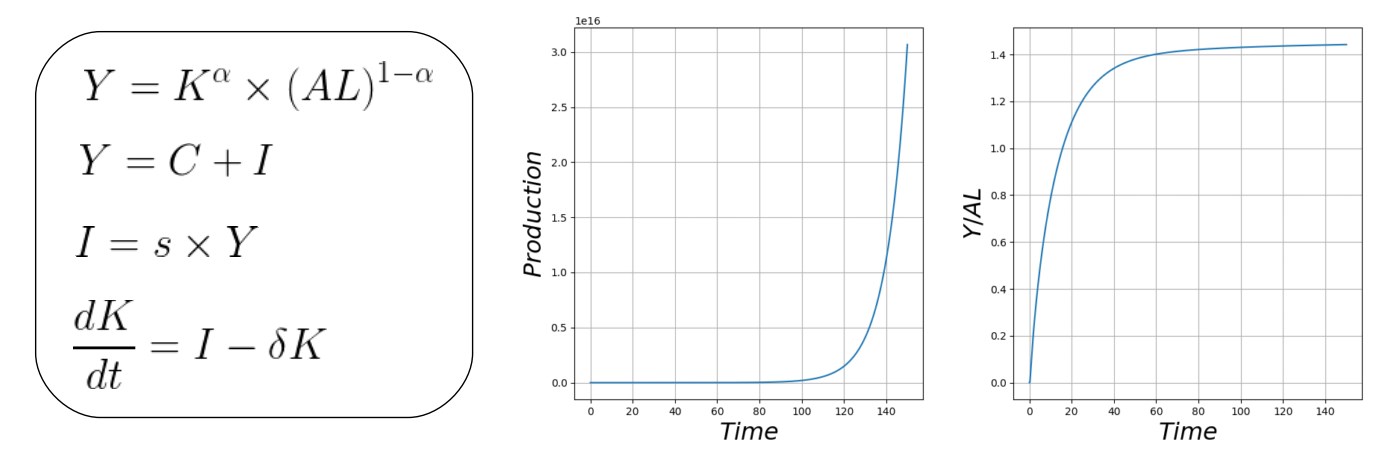
Le modèle de Solow, créé en 1956, est un modèle macroéconomique qui explique la croissance par l’ accumulation du capital, la croissance de la population active, et la croissance de la productivité du travail. C’ est un modèle de référence de l’économie néo-classique.
Il utilise une fonction de production de Cobb-Douglas a deux facteurs :
\[Y=K^{\alpha}(AL)^{1-\alpha}\]avec :
\(Y\) la production
\(K\) le capital
\(A\) la productivité du travail
\(L\) la population active
La productivité du travail augmente de maniere exogene, au taux g\(_{A }\).
La population active augmente également de maniere exogene. Dans notre modèle, on choisit de faire tendre la population active vers une valeur limite P\(_{L}\): le taux de croissance de la population active est \(g_{L}=q(1-L/P_{L})\). Le taux de croissance diminue a mesure que la population active L se rapproche de sa valeur limite P\(_{L}\).
Le capital s’érode au taux \(\delta K\), érosion compensée par l’ investissement I.
\(dK/dt=I-\delta K\)
Une part s de la production est réinvestie :
[\ I=sY\
]
Dans ce modèle, la production Y augmente exponentiellement, grâce a la croissance de la productivité du travail. La production par unité de travail effectif Y/AL converge vers un état stationnaire.
On utilise la fonction de production du modèle de Solow comme fonction de requête de production (section 1.2.1).
On initialise les requêtes de production de chaque bien final au lancement de la simulation. A chaque instant, on calcule la requête pour l’instant t+dt à partir du résultat de production de l’instant t
\(Y_{REQ}(t+dt)=Y(t)\ast\left( \frac{K(t+dt)}{K(t)}\right) ^{\alpha}\left( \frac{A(t+dt)L(t+dt)}{A(t)L(t)}\right) ^{1-\alpha}\) avec
\(Y_{REQ}\) la requête de production adressée a la sphère physique.
\(Y\) la production effective (qui peut différer de la requête de production)
Ainsi, tant que la requête de production est satisfaite, la production est égale à celle prédite par le modèle de Solow. Si la requête de production n’est pas satisfaite à l’instant t, la requête à l’instant t+dt s’adapte : on ne continue pas à demander une croissance exponentielle indéfiniment alors que la production effective ne suit plus.
L’investissement est défini pour chaque feuille ressource. On définit un paramètre s commun à toutes les feuilles, qui correspond à la fraction de la production réinvestie. La production de chaque feuille correspond à ce qui a été effectivement utilisé par le noyau central de le sphère physique, c’est à dire la variable \(G_{USED}\).
Ainsi,
[I=sG_{USED}%]
Pour la requête de recyclage, on définit la loi suivante : on souhaite recycler une proportion constante de la quantité de déchets produits On définit cette proportion à l’initialisation de la simulation., en indiquant la valeur du paramètre recycling compris entre 0 et 1.
L’équation de la requête de recyclage est donc :
\[Y_{REQ}(t+dt)=(F_{LP}(t)+G_{USED}(t))\ast recycling\]Cette loi n’est qu’une proposition. On pourrait également tenir compte de la quantité totale de déchets \(X_{L}\) pour la requête de recyclage, et non pas simplement de la variation de cette quantité.
Il a été choisi de ne pas faire varier le niveau cible de stock demandé aux feuillets, ni le mix énergétique souhaité, ni les quantités de ressources nécessaires à la production d’une unité de chaque bien final (coefficients de la matrice des recettes). Le modèle a été créé dans un souci de permettre à l’utilisateur de proposer et tester ses propres fonctions et scénarios de variation de toutes ces requêtes de la sphère économique à la sphère physique. Ainsi, la partie contenant toutes les fonctions accessibles à l’utilisateur est située dans un fichier à part, court et commenté.
Ce modèle n’a pas pour but de reproduire le plus fidèlement possible la trajectoire de l’économie mondiale des dernières décennies, ni de prédire quantitativement ce qui pourrait advenir. Il s’agit d’un outil permettant de tester une multitude d’hypothèses, de scénarios, de modèles macro-économiques dans un cadre prenant en compte explicitement l’impact de l’activité économique sur la sphère physique et les rétroactions de celle-ci.
Le nombre d’hypothèses et scénarios pouvant être testés n’est limité que par l’imagination de l’utilisateur. Par conséquent, cette partie n’a pas pour ambition de livrer une analyse complète de ce que l’on peut tirer du modèle, mais de livrer quelques résultats fondamentaux obtenus. On tachera de présenter ces résultats, puis de les illustrer au moyen d’un exemple qui permet d’isoler le phénomène ou motif discuté.
On retrouve des résultats attendus, mais qui ne sont pas obtenus par la plupart des modèles macroéconomiques. Cela permet de vérifier que cet outil atteint son objectif de proposer une base physique aux modèles macroéconomiques via la prise en compte directe des flux de matière et d’énergie engendrés par l’activité économique.
On observe, selon le paramétrage de la situation, des rétroactions de la sphère physique sur l’activité économique. En particulier, lorsque le flux de recyclage (naturel ou humain) est nul (ressources non recyclables par exemple) ou insuffisant, on observe l’épuisement des ressources “stock”, et leur rétroaction sur la production. Cette rétroaction prend la forme de rupture de pentes : il s’agit donc d’effondrement davantage que de diminution progressive. Illustrons ce point par un exemple jouet qui permet de faire apparaître le mécanisme de l’effondrement.
On considère un monde à trois ressources, cuivre, bois et pétrole. Ces trois ressources permettent de produire deux biens finaux, selon les recettes :
cuivre + énergie = bien 0
cuivre + bois + énergie = bien 1
Par souci de simplicité, on considère que l’on n’est pas capable de recycler le cuivre (ou que l’on ne le souhaite pas). Le bois se recycle naturellement. On suppose également que les résistances des appareils de production sont constantes (érosion du capital et investissement nuls)
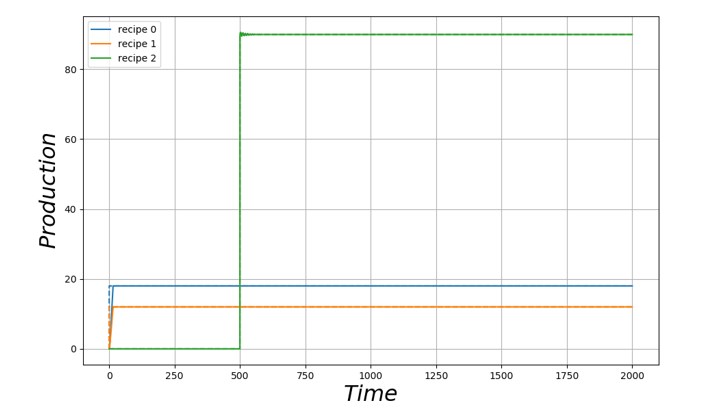
Enfin, on se place dans un scénario de croissance nulle. La demande en biens finaux est constante (respectivement 12 bien 0 et 18 bien 1 par unité de temps).
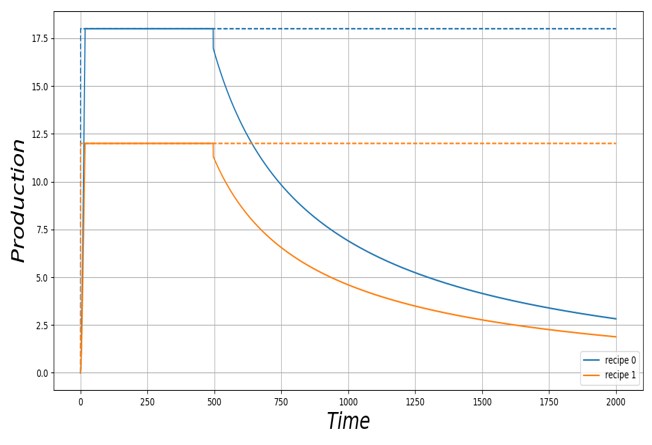
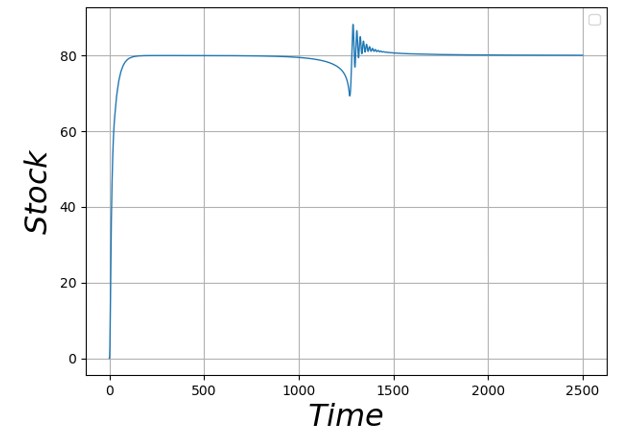
On observe une chute de la production des biens 1 et 2 à t=500, malgré une requête de production constante. La production semble converger exponentiellement vers une production nulle (ce qui est confirmé par un passage en échelle logarithmique).
Les ressources cuivre et pétrole (seule ressource énergétique de la simulation) sont communes aux deux recettes de production. La simultanéité des chutes de production des biens 0 et 1 suggère que l’une de ces deux ressources à fait défaut.
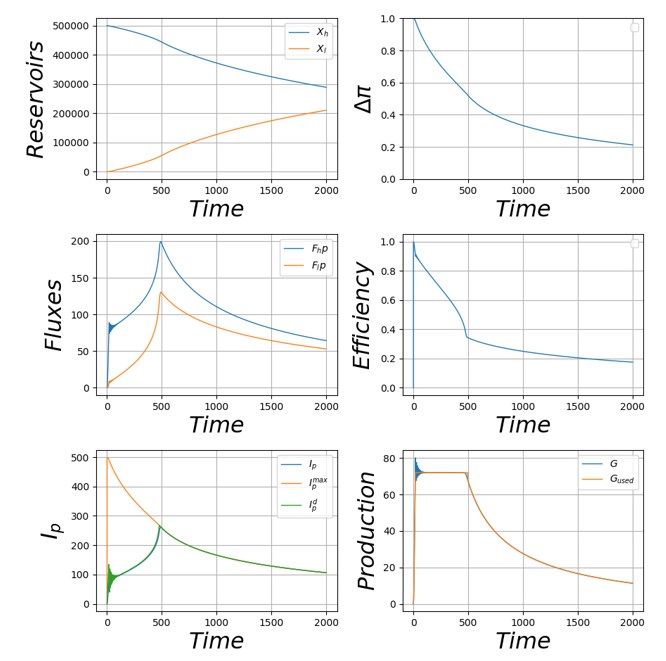
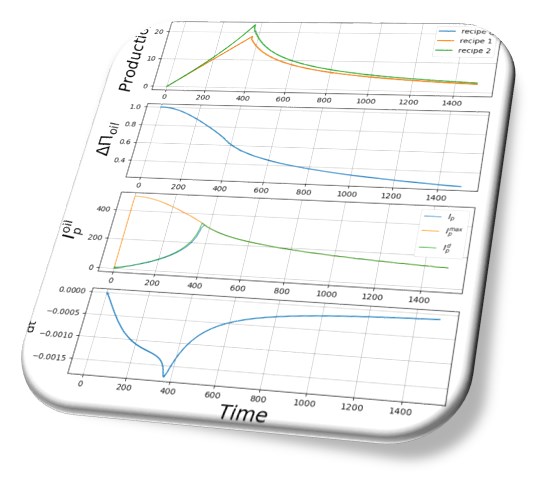
En effet, l’état de la ressource pétrole semble s’être dégradé rapidement, entraînant une chute de la production de pétrole à t=500. Examinons le mécanisme menant à cet effondrement.
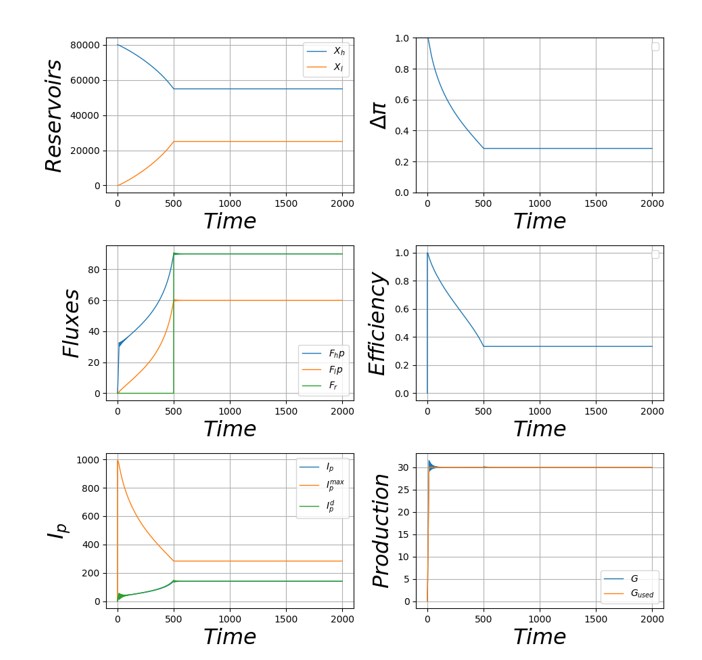
La figure 8a indique que le réservoir haut se vide progressivement, tandis que le réservoir bas se remplit. En conséquence, la différence de potentiels diminue (figure 8b). Malgré une requête de production constante, les flux de pétrole venant du réservoir haut (FHP) et en direction du réservoir bas (FLP) augmentent rapidement, à cause du pincement des potentiels (figure 8c). Dans le même temps, l’efficacité du processus chute (figure 8d). L’intensité de production augmente pour compenser la chute de l’efficacité et satisfaire la requête. L’intensité de production maximale possible diminue, et à t=500, l’intensité de production atteint l’intensité de production maximale (figure 8e). Immédiatement, la production chute (figure 8f).
Ainsi, un scénario de croissance nulle, sans recyclage, entraîne un emballement avec une explosion des flux de ressource afin de compenser la perte d’efficacité, dans un cercle vicieux. On observe ici un défaut de production lié à l’épuisement d’une ressource non-renouvelable et non-substituée.
Cependant, une activité économique stable (qui ne s’effondre pas à temps infini) est possible, si elle n’implique l’utilisation que de ressources stock recyclables (naturellement ou humainement) et de ressources renouvelables (ressources flux).
Pour illustrer ce point, on se place dans une situation similaire à l’exemple précédent, en remplaçant la feuille “pétrole” par une feuille “énergie solaire”. La demande en biens finaux 0 et 1 est constante. On suppose que la ressource bois est très abondante, contrairement à la ressource cuivre. Cependant, on est capable de recycler le cuivre, au moyen d’un apport d’énergie : une unité d’énergie permet de recycler une unité de cuivre.
On suppose également que la surface de panneaux solaires installée est très importante, et qu’il n’y a pas d’érosion du capital. Ainsi, la quantité d’énergie renouvelable est largement supérieure aux besoins de l’activité économique. C’est une hypothèse forte.
De \(t=0\) à \(t=500\), on décide de ne pas recycler le cuivre. \(At=500\) et pour tous les instants ultérieurs, on décide de recycler 100 % des déchets de cuivre nouvellement produit.
Le système semble stable (Fig. [Fig9]). Mais l’observation de l’évolution de l’état de la ressource cuivre montre que la décision de fixer une requête de recyclage de 100 % à t=500 à permis d’éviter un effondrement, et d’atteindre cet état stable (Fig. [Fig10]).
[Fig9]
[Fig10]
Il existe donc, pour un ensemble de ressources et de recettes donnée, un niveau de production stable maximum. L’activité économique peut dépasser ce niveau stable maximum grâce à l’usage de ressources “stock” dont le rythme d’exploitation est virtuellement illimité. Mais si l’exploitation de ces ressources est plus rapide que le recyclage naturel, ou si elle ne s’accompagne pas d’une augmentation égale du recyclage humain (en particulier si celui-ci est impossible, comme pour les ressources fossiles), on risque de dégrader ces ressources, si bien que le nouvel état n’est pas stable.
En fin de compte, les facteurs limitant sont :
l’utilisation de ressources stock que l’on ne sait pas recycler, et pour lesquelles on ne trouve pas de substituts.
La production d’énergie renouvelable, nécessaire au recyclage de toutes les autres ressources stock.
Si les ressources stock s’épuisent, on revient de manière forcé à un niveau stable, vérifiant les conditions énoncées précédemment (section 2.2). La dégradation de l’état des ressources stock advenue est irréversible, et le nouveau niveau de production stable maximum a diminué.
Afin d’illustrer ces propos, on considère un monde à quatre ressources : cuivre, bois, pétrole et énergie solaire. Par souci de simplicité, on suppose à nouveau que l’on ne sait pas recycler le cuivre, mais que cette ressource est extrêmement abondante. On suppose également que le taux de régénération du bois est très élevé.
On considère les mêmes recettes que précédemment (section 2.1). La requête de production des biens finaux suit une trajectoire de croissance exponentielle obtenue par une loi de type “Solow” , semblable à celle décrite en section 1.2.2.2. Les requêtes de production initiales sont proches de zéro.
Le mix énergétique souhaité est : 100 % d’énergie solaire. Le mix énergétique réel peut être différent, si le mix énergétique souhaité ne permet pas de répondre aux requêtes de production.
[Fig11]
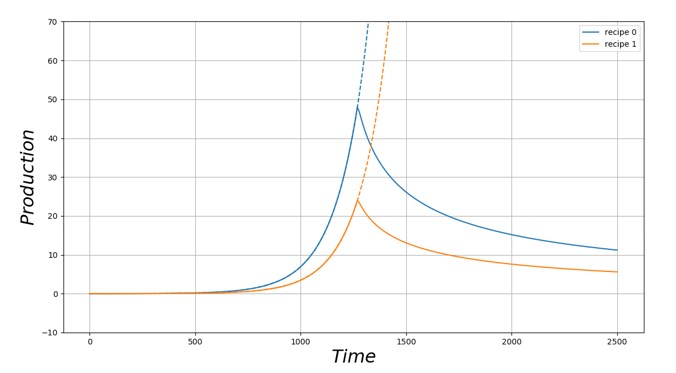
On observe (Fig. [Fig11]) dans un premier temps une augmentation exponentielle de la production de biens 1 et 2, suivant la croissance exponentielle des requêtes de production. A t=1250, la production de biens 1 et 2 chute, et les requêtes de production ne sont plus satisfaites. Les flux de production semblent converger vers un niveau plus faible mais non-nul.
[Fig12]
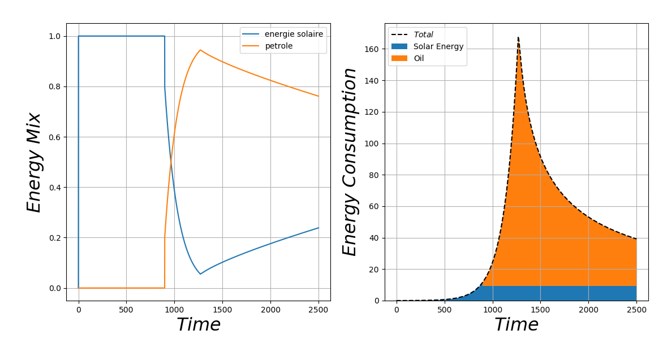
L’étude de l’évolution du mix énergétique réel au cours du temps indique que dans un premier temps (t \(<\) 800), le besoin en énergie est entièrement couvert par la feuille “énergie solaire” (Fig. [Fig12]). Le mix énergétique réel est donc égal au mix énergétique souhaité. Pour t \(>\) 800, le besoin en énergie dépasse la production d’énergie solaire. On fait donc appel à la feuille pétrole afin de continuer à satisfaire la requête en énergie. Le mix énergétique réel voit la place du pétrole devenir prépondérante, à mesure que la demande en énergie croit. La feuille pétrole permet donc de continuer à suivre la trajectoire de croissance exponentielle au-delà du niveau permis par l’utilisation unique de l’énergie solaire. A t=1250, la production de pétrole chute, ce qui semble indiquer un défaut de production de la feuille. Un regard sur l’évolution de l’état de la feuille pétrole le confirme. La production de biens finaux chute, suivant la production de pétrole. Le mix énergétique revient peu à peu vers un mix 100 % solaire. Les niveaux de production convergent vers le niveau maximal permis par le flux d’énergie solaire disponible.
Toutes les illustrations jusqu’ici proviennent de simulations avec capital fixé : le taux d’érosion du capital
était nul, et l’investissement également. Ainsi, les résistances \(R_{P}\) des feuilles stock et paramètres “`surface installée “`des feuilles flux étaient constantes. L’introduction d’un taux d’érosion et d’un investissement non-nul modifie les trajectoires observées.
Dans la suite, on suppose que l’investissement dans le capital d’une feuille est une proportion fixe de la production de cette feuille : le secteur “ vend “ x unités de ressource, et en réinvestit une proportion s. C’est la loi d’investissement décrite en section 1.2.2.2. Notons que les résultats présentés ci-après dépendent fortement de cette loi d’investissement. En particulier, il serait judicieux d’écrire une loi modélisant une situation ou le secteur A peut choisir d’investir une part de ses revenus dans le secteur B si celui-ci est plus “ rentable “. Toute la démarche du projet consiste à laisser accessible à l’utilisateur la partie de modélisation économique afin de lui permettre, par exemple, de tester une telle loi.
Les notions d’érosion du capital et d’investissement entraînent l’apparition de cercles vertueux et de cercles vicieux dans un contexte de requête de production croissante.
Tant que la production augmente, l’investissement augmente. Le capital augmente donc également, et la résistance RP diminue. Le terme de friction diminue donc, et la valeur maximal du flux produit GMAX augmente. La production peut donc augmenter encore d’avantage, et ainsi de suite.
A l’inverse, si la production chute, l’investissement chute, donc le capital également, et la résistance augmente, ce qui aggrave encore la chute de la production.
Pour illustrer ces propos, on considère un monde à trois ressources : cuivre, bois, pétrole, et deux recettes (les mêmes que précédemment). Le cuivre et le bois sont supposés très abondants. La requête de production est exponentiellement croissante. On effectue deux simulations successives, une avec érosion du capital et investissement nuls, une seconde avec érosion du capital et investissement positifs (Fig. [Fig13]).
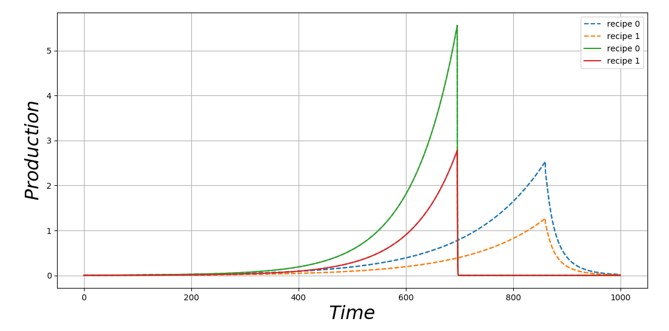[Fig13]
On constate que la croissance et la décroissance sont bien plus rapide dans la simulation avec investissement et érosion du capital. On peut l’expliquer en examinant l’évolution de l’état de la feuille pétrole.
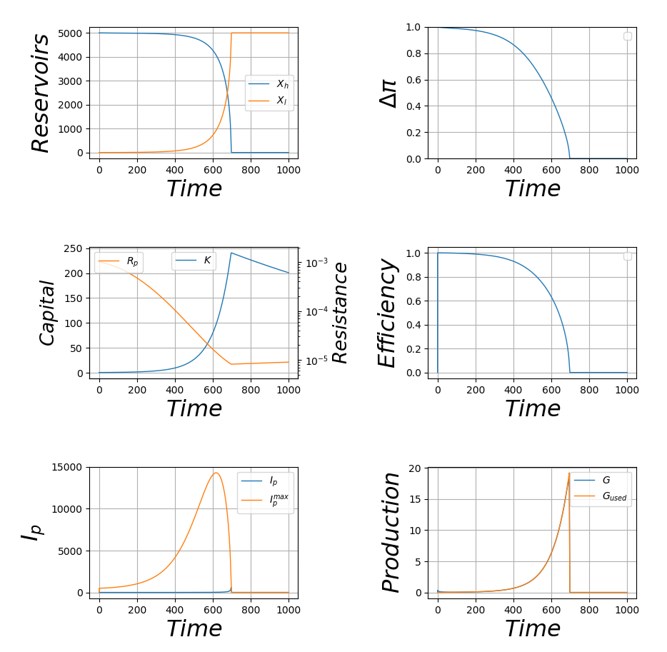[Fig14]
De t=0 à t=700, la production de pétrole augmente, en réponse à l’augmentation exponentielle des requêtes. L’investissement augmente donc, ce qui permet d’augmenter le capital et de diminuer la résistance (Fig. [Fig14]c). Par conséquent, l’intensité de production maximale possible augmente (Fig. [Fig14]e). De plus, la diminution de la résistance compense la chute de la différence de potentiel (Fig. [Fig14]b). Ainsi, on parvient à extraire presque toute la ressource du réservoir haut (Fig. [Fig14]a). A \(t=700\), le réservoir haut est presque vide. Malgré la faible valeur de la résistance, la production chute.
On rentre alors dans un cercle vicieux : l’investissement chute également, et ne parvient plus à compenser l’érosion du capital. La résistance de l’appareil de production augmente à nouveau, et la production ultérieure est encore plus difficile. La chute s’accélère.
EcoDyco est déposé sous licence GPL V3
Boulding, K.E. The economics of the coming spaceship earth. In Environmental Quality in a Growing Economy.H. Jarrett, Ed.: 3–14. Johns Hopkins University Press. Baltimore, 1966.
Georgescu-Roegen, N. The Entropy Law and the Economic Process. Harvard University Press. Cambridge, MA, 1971.
Fritz Söllner, A reexamination of the role of thermodynamics for environmental economics, Ecological Economics, Volume 22, Issue 3, Pages 175-201, 1997.
Cutler J Cleveland, Matthias Ruth, When, where, and by how much do biophysical limits constrain the economic process?: A survey of Nicholas Georgescu-Roegen’s contribution to ecological economics, Ecological Economics, Volume 22, Issue 3, Pages 203-223, 1997.
Herman E Daly, Georgescu-Roegen versus Solow/Stiglitz, Ecological Economics, Volume 22, Issue 3, Pages 261-266, 1997.
Robert M Solow, Georgescu-Roegen versus Solow-Stiglitz, Ecological Economics, Volume 22, Issue 3, Pages 267-268, 1997.
Joseph E Stiglitz, Georgescu-Roegen versus Solow/Stiglitz, Ecological Economics, Volume 22, Issue 3, Pages 269-270, 1997.
Herman E Daly, Reply to Solow/Stiglitz, Ecological Economics, Volume 22, Issue 3, Pages 271-273, 1997,
Meadows, D. H., Meadows, D.H., Randers, Jørgen, et al. The limits to growth: a report to the club of Rome (1972). 1972.
Glucina, M. D. and Mayumi, K, Connecting thermodynamics and economics. Annals of the New York Academy of Sciences, 1185: 11-29. (2010)
Godard O., Baillon J., Céron J., Substitutions et économie sociale des ressources naturelles, page 15, 1980
La question de la capacité d’une croissance indéfinie trouve donc là ses principaux ingrédients, à savoir:
La baisse des rendements en fonction de l’intensité de prélèvement, au delà d’un certain seuil.
La baisse de la production et des en présence de pincement de la disponibilité de la ressource. est présent au cœur du mécanisme de chacun des feuillets. Il apparaît donc que le flux d’extraction des ressources dépend à la fois des capacités de production via \(R_{P}\) installées et de la différence de potentiel \(\Delta\Pi\).
Au minimum un feuillet énergie et un feuillet matière.
Attention, la lecture des paramètres dans les fichiers est peu robuste. Il faut veiller a respecter l’espacement, ne pas rajouter un saut de ligne a la fin, etc. En particulier, les chaînes de caractere du tableau cell (par exemple “ cuivre ”) servent ensuite a rediriger vers le fichier “ cuivre ”.txt pour l’initialisation de la feuille cuivre. Le nom du fichier contenant les paramètres de la feuille doit donc etre la même chaîne de caractere que celle qui apparaît dans cell/
Remarquons que ce choix de modélisation est peu réaliste. Non seulement il faut en général d’autres ressources que juste de l’énergie pour opérer un processus de recyclage, mais la difficulté a recycler (c’est a dire la quantité d’énergie a apporter pour recycler une unité de ressource) varie, selon la qualité du déchet. Ce point sera a améliorer dans la suite du développement du modèle.
Dans une première tentative, le noyau central indique (a chaque nouveau pas de temps) à chaque feuille le niveau de production souhaité. Le noyau central doit donc recueillir depuis les feuilles les informations concernant les quantités de ressources disponible pour utilisation \((X_{S})\), les traiter, puis renvoyer a chaque feuille le niveau de production requis pour l’instant suivant. La complexité de ce processus augmente exponentiellement avec le nombre de ressources et le nombre de recettes. Finalement, il a été impossible de réaliser un algorithme satisfaisant permettant de traiter toutes ces données, car un tel algorithme nécessite l’introduction de multiples tests conditionnels qui rendent le processus tres peu stable. Remarquons enfin que ce fonctionnement est peu naturel (dans un systeme de marchés), puisqu’il correspond a l’hypothèse d’une entité centrale régulatrice qui indique a chaque secteur de production le niveau de production requis en fonction des résultats des autres secteurs.
Par exemple, dans les années 1970, la demande en nickel a chuté de 20%, principalement a cause de la substitution du manganese au nickel dans la production de pare-chocs automobiles.